练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用min{a，b}表示a、b两数中的最小值，若函数f(x)＝min{|x|，|x＋t|}的图象关于直线x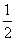＝－对称，则t的值为(　　)

    A．－2                                                          B．2

    C．－1                                                          D．1


    　D

    [解析]　如图，要使f(x)＝min{|x|，|x＋t|}的图象关于直线x＝－对称，则t＝1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设，，若是单调递减数列，则实数的取值范围为______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     把下列在平面内成立的结论类比地推广到空间，仍然正确的是                 (　　)

      A. 如果一条直线与两条平行线中的一条相交，则必与另一条相交

      B. 如果一条直线与两条平行线中的一条垂直，则必与另一条垂直

      C. 如果两条直线与第三条都不相交，则这两条直线不相交

      D. 如果两条直线同时与第三条直线垂直，则这两条直线平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝(m2－m－1)xm2－2m－3是幂函数，且在(0，＋∞)上是减函数，则实数m的值为(　　)

    A．2　　　　B．3　　　　C．4　　　　D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝若方程f(x)＝x＋a有且只有两个不相等的实数根，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若二次函数f(x)＝ax2＋bx＋c(a≠0)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

    (1)求f(x)的解析式；

    (2)若在区间[－1,1]上，不等式f(x)>2x＋m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知二次函数f(x)＝ax2＋bx＋c(a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，有f(x)≤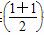2.

    (1)求f(1)的值；

    (2)证明a>0，c>0；

    (3)当x∈[－1,1]时，函数g(x)＝f(x)－mx(x∈R)是单调函数，求证：m≤0或m≥1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    当前环境问题已成为问题关注的焦点，2009年哥本哈根世界气候大会召开后，为减少汽车尾气对城市空气的污染，某市决定对出租车实行使用液化气替代汽油的改装工程，原因是液化气燃烧后不产生二氧化硫、一氧化氮等有害气体，对大气无污染，或者说非常小．请根据以下数据：①当前汽油价格为2.8元/升，市内出租车耗油情况是一升汽油大约能跑12km；②当前液化气价格为3元/千克，一千克液化气平均可跑15～16km；③一辆出租车日平均行程为200km.

    (1)从经济角度衡量一下使用液化气和使用汽油哪一种更经济(即省钱)；

    (2)假设出租车改装液化气设备需花费5000元，请问多长时间省出的钱等于改装设备花费的钱．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F1、F2分别是椭圆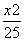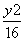＋＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点的距离为(　　)

    A．4                               B．3

    C．2                               D．5

    查看答案和解析>>

    同步练习册答案