
分析 (1)利用平面向量数量积的运算,两角和的正弦函数公式化简可得f(x)=sin(ωx+φ),利用周期公式可求ω,将点P($\frac{π}{6},1$)代入y=sin(2x+φ),结合范围|φ|<$\frac{π}{2}$,可求φ,即可得解函数f(x)的解析式.
(2)由题意可得sin(2C+$\frac{π}{6}$)=-1,结合范围0<C<π,可得C=$\frac{2π}{3}$.由$\overrightarrow{CA}•\overrightarrow{CB}=-\frac{3}{2}$,解得ab=3,利用余弦定理即可解得c的值.
解答 (本小题满分12分)
解:f(x)=$\overrightarrow{m}•\overrightarrow{n}$=sinωxcosφ+cosωxsinφ=sin(ωx+φ),----------(2分)
由题意,得$\frac{T}{4}$=$\frac{5π}{12}$-$\frac{π}{6}$,可得:T=π,所以ω=2.----------------(3分)
将点P($\frac{π}{6},1$),代入y=sin(2x+φ) 得sin(2×$\frac{π}{6}$+φ)=1,
所以φ=2kπ+$\frac{π}{6}$,(k∈Z),
又因为|φ|<$\frac{π}{2}$,
所以φ=$\frac{π}{6}$,------------(5分)
即函数f(x)的解析式为f(x)=sin(2x+$\frac{π}{6}$),(x∈R)--------------(6分)
(2)由f(C)=-1,即sin(2C+$\frac{π}{6}$)=-1,
又因为0<C<π,可得:C=$\frac{2π}{3}$.------(8分)
由$\overrightarrow{CA}•\overrightarrow{CB}=-\frac{3}{2}$,知abcosC=-$\frac{3}{2}$,
所以,ab=3.----------------(10分)
由余弦定理知c2=a2+b2-2abcosC=(a+b)2-2ab-2abcosC=(2$\sqrt{3}$)2-2×3-2×3×(-$\frac{1}{2}$)=9,
所以c=3或-3(舍去),故c=3.--------------------(12分)
点评 本题主要考查了平面向量数量积的运算,两角和的正弦函数公式,周期公式,余弦定理的综合应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
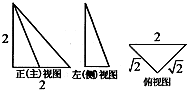
| A. | 2 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}+\sqrt{3}$+3 | D. | $\sqrt{3}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | -$\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 8 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com