
分析 由题意求出SA=AC=SB=BC=$\sqrt{2}$R,∠SAC=∠SBC=90°,说明球心O与AB的平面与SC垂直,求出OAB的面积,利用棱锥S-ABC的体积,求出R,即可求球O的体积.
解答 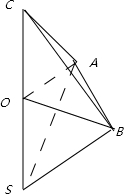 解:如图:由题意,设球的直径SC=2R,A,B是该球球面上的两点.
解:如图:由题意,设球的直径SC=2R,A,B是该球球面上的两点.
AB=2,∠ASC=∠BSC=45°,求出SA=AC=SB=BC=$\sqrt{2}$R,
∠SAC=∠SBC=90°,所以平面ABO与SC垂直,则S△ABO=$\frac{\sqrt{3}}{4}{R}^{2}$
进而可得:VS-ABC=VC-AOB+VS-AOB,
所以棱锥S-ABC的体积为:$\frac{1}{3}•\frac{\sqrt{3}}{4}{R}^{2}$•2R=$\frac{4\sqrt{3}}{3}$,
所以R=2,
此时三角形AOB为正三角形,符合,
所以球O的体积为$\frac{32}{3}π$.
故答案为$\frac{32}{3}π$.
点评 本题是基础题,考查球的内接三棱锥的体积,考查空间想象能力,计算能力,球心O与AB的平面与SC垂直是本题的解题关键,常考题型.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
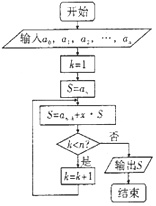 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )
秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的a0,a1,a2,…,an分别为0,1,2,…,n,若n=5,根据该算法计算当x=2时多项式的值,则输出的结果为( )| A. | 248 | B. | 258 | C. | 268 | D. | 278 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
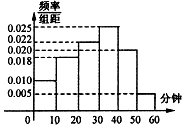 北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
北京时间3月15日下午,谷歌围棋人工智能AlphaGo与韩国棋手李世石进行最后一轮较量,AlphaGo获得本场比赛胜利,最终人机大战总比分定格在1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.| 非围棋迷 | 围棋迷 | 合计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(x2≥k0) | 0.05 | 0.010 |
| k0 | 3.74 | 6.63 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e2-3,e2+1) | B. | (e2-3,+∞) | C. | (-∞,2e2+2) | D. | (2e2-6,2e2+2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com