
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)求实数![]() 的值;
的值;
(2)若![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 且
且![]()
![]() 上最小值为
上最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据奇函数定义确定![]() ,代入可得实数
,代入可得实数![]() 的值,再利用定义证明
的值,再利用定义证明![]() 时,函数为奇函数,(2)先研究函数单调性:为
时,函数为奇函数,(2)先研究函数单调性:为![]() 上的单调递增函数,再利用奇函数和单调性转化不等式
上的单调递增函数,再利用奇函数和单调性转化不等式
![]() ,最后再根据一元二次不等式恒成立,利用判别式恒负求实数
,最后再根据一元二次不等式恒成立,利用判别式恒负求实数![]() 的取值范围;(3)先根据条件
的取值范围;(3)先根据条件![]() ,解出
,解出![]() 的值.再根据
的值.再根据![]() 与
与![]() 的关系,将函数
的关系,将函数![]() 转化为一元二次函数,根据对称轴与定义区间位置关系讨论最小值取法,最后由最小值为
转化为一元二次函数,根据对称轴与定义区间位置关系讨论最小值取法,最后由最小值为![]() ,求出
,求出![]() 的值.
的值.
试题解析:解:(1)因为![]() 是定义域为
是定义域为![]() 的奇函数,所以
的奇函数,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
(2)由(1)知:![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() 且
且![]() ,所以
,所以![]() ,
,
所以![]() 是
是![]() 上的单调递增,
上的单调递增,
又![]() 是定义域为
是定义域为![]() 的奇函数,
的奇函数,
所以![]()
即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,即
,即![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)因为![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
所以![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,所以
,所以![]() ,
,
因为![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
因为![]() 的对称轴为
的对称轴为![]()
所以当![]() 时,
时, ![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
当![]() 时,
时, ![]() ,解得
,解得![]() ,
,
综上可知:![]() .
.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的极坐标方程;
的极坐标方程;
(2)求直线![]() 与圆
与圆![]() 的交点的极坐标.
的交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.

(1)若日均收看该体育节目时间在![]() 内的观众中有两名女性,现从日均收看时间在
内的观众中有两名女性,现从日均收看时间在![]() 内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错概率不超过
人,完成答题卡中的列联表并判断能否在犯错概率不超过![]() 的前提下认为是体育迷与性别有关系吗?
的前提下认为是体育迷与性别有关系吗?
附表及公式:
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校600名文科学生参加了4月25日的三调考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从抽取100名学生的成绩进行统计分析,将学生编号为000,001,002,…599
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(上面是摘自随机数表的第4行到第7行);
(2)抽出的100名学生的数学、外语成绩如下表:
外语 | ||||
优 | 良 | 及格 | ||
数学 | 优 | 8 | m | 9 |
良 | 9 | n | 11 | |
及格 | 8 | 9 | 11 | |
若数学成绩优秀率为35%,求m,n的值;
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为  ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(Ⅰ)写出C的普通方程;
(Ⅱ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.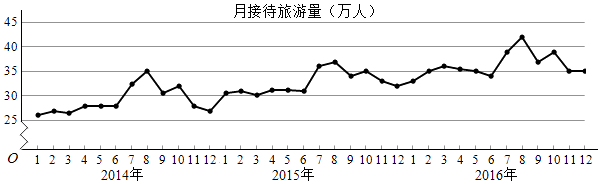
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
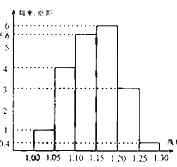
(Ⅰ)在答题卡上的表格中填写相应的频率;
(Ⅱ)估计数据落在(1.15,1.30)中的概率为多少;
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com