
 ������Ⱦ���ֳ�Ϊ������Ⱦ����ָ������������Ȼ��������ijЩ���ʽ�������У����ֳ��㹻��Ũ�ȣ��ﵽ�㹻��ʱ�䣬�����Σ������������ʡ�����������������ȫ����ҲԽ��Խ��ע�����������⣮��������Ⱦָ������λ����g/m3��Ϊ0��50ʱ��������������Ϊһ������������״�������ţ���������Ⱦָ��Ϊ50��100ʱ��������������Ϊ��������������״������������������Ⱦָ��Ϊ100��150ʱ����������������Ϊ��������������״�����������Ⱦ����������Ⱦָ��Ϊ150��200ʱ��������������Ϊ�ļ�����������״�������ж���Ⱦ����������Ⱦָ��Ϊ200��300ʱ��������������Ϊ�弶����������״�������ض���Ⱦ����������Ⱦָ��Ϊ300����ʱ��������������Ϊ��������������״������������Ⱦ.2015��8��ij��ijʡx����������ͳ�����£�
������Ⱦ���ֳ�Ϊ������Ⱦ����ָ������������Ȼ��������ijЩ���ʽ�������У����ֳ��㹻��Ũ�ȣ��ﵽ�㹻��ʱ�䣬�����Σ������������ʡ�����������������ȫ����ҲԽ��Խ��ע�����������⣮��������Ⱦָ������λ����g/m3��Ϊ0��50ʱ��������������Ϊһ������������״�������ţ���������Ⱦָ��Ϊ50��100ʱ��������������Ϊ��������������״������������������Ⱦָ��Ϊ100��150ʱ����������������Ϊ��������������״�����������Ⱦ����������Ⱦָ��Ϊ150��200ʱ��������������Ϊ�ļ�����������״�������ж���Ⱦ����������Ⱦָ��Ϊ200��300ʱ��������������Ϊ�弶����������״�������ض���Ⱦ����������Ⱦָ��Ϊ300����ʱ��������������Ϊ��������������״������������Ⱦ.2015��8��ij��ijʡx����������ͳ�����£�| ������Ⱦָ�� ����λ����g/m3�� | [0��50] | ��50��100] | ��100��150] | ��150��200] |
| ������� | 15 | 40 | y | 10 |
���� ��1������Ƶ�ʷֲ�ֱ��ͼ������Ƶ��=$\frac{Ƶ��}{��������}$�����x��y��ֵ������ֱ��ͼ�и�С���ж�Ӧ�ĸߣ���ȫƵ�ʷֲ�ֱ��ͼ��
��2�������оٷ���������¼����������Ӧ�ĸ��ʼ��ɣ�
��� �⣺��1����$0.003��50=\frac{15}{x}$����x=100��
��15+40+y+10=100����y=35.$\frac{40}{100��50}=0.008$��$\frac{35}{100��50}=0.007$��$\frac{10}{100��50}=0.002$��
Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��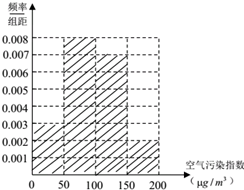
��2���ڿ�����Ⱦָ��Ϊ50��100��150��200�ļ����зֱ��ȡ4����1�����㣬�������Ⱦָ��Ϊ50��100��4������ֱ��Ϊa��b��c��d��������Ⱦָ��Ϊ150��200��1�������ΪE��������ȡ2���Ļ����¼��ֱ�Ϊ��a��b������a��c������a��d������a��E������b��c������b��d������b��E������c��d������c��E������d��E����10�֣������¼�A��������Ϊ���������Ļ����¼�Ϊ��a��b������a��c������a��d������b��c������b��d������c��d����6�֣������¼�A��������Ϊ���������ĸ�����$P��A��=\frac{6}{10}=\frac{3}{5}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬Ҳ���������оٷ���ŵ���͵ĸ������⣬�ǻ�����Ŀ��


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{\sqrt{6}}{4}$ | C�� | 4$\sqrt{3}$ | D�� | 4$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{11}$ | B�� | $\frac{10}{11}$ | C�� | $\frac{9}{10}$ | D�� | $\frac{11}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{4}$ | B�� | $\frac{4}{5}$ | C�� | $-\frac{4}{5}$ | D�� | $-\frac{5}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
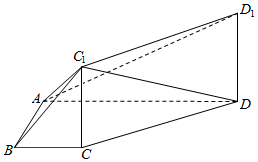 ��ͼ���ı���ABCD�����Σ�AD��BC����BAD=90�㣬DD1����ABCD��DD1��CC1��AD=4��AB=2��BC=1��
��ͼ���ı���ABCD�����Σ�AD��BC����BAD=90�㣬DD1����ABCD��DD1��CC1��AD=4��AB=2��BC=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | -$\frac{\sqrt{3}}{2}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com