
已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2, .
.
(1)若b=4,求sin A的值;
(2)若△ABC的面积S△ABC=4,求b,c的值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为 sinC,求角C的度数.
sinC,求角C的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1).设AD=x(x≥0),DE=y,求用x表示y的函数关系式,并求函数的定义域;
(2).如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·郧阳模拟)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)(a-b+c)=ac.
(1)求B.
(2)若sinAsinC= ,求C.
,求C.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
火车站 北偏东
北偏东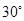 方向的
方向的 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得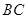 距离为31
距离为31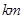 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达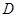 处,测得离电视塔21
处,测得离电视塔21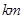 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com