
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为 sinC,求角C的度数.
sinC,求角C的度数.
(1)c= ;(2) ∠C=60°.
;(2) ∠C=60°.
解析试题分析:(1)由正弦定理可知: sinA+sinB= sinC等价于a+b=
sinC等价于a+b= c代入已知a+b+c=
c代入已知a+b+c= +2可求得边c的长; (2)由三角形的面积公式可得S△ABC=
+2可求得边c的长; (2)由三角形的面积公式可得S△ABC= absinC=
absinC= sinC,又注意到sinC>0得ab=
sinC,又注意到sinC>0得ab=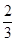 ,结合(1)中结论,并注意到a+b=2,应用余弦定理cosC=
,结合(1)中结论,并注意到a+b=2,应用余弦定理cosC=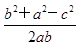 =
=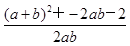 可求得cosC值,进而得到角C的度数.
可求得cosC值,进而得到角C的度数.
试题解析:(1)在△ABC中,∵sinA+sinB= sinC,
sinC,
由正弦定理,得a+b= c, 3分
c, 3分
∴a+b+c= c+c=(
c+c=( +1)c=
+1)c= +2.
+2.
∴a+b=2,c= 6分。
6分。
(2)在△ABC中,S△ABC= absinC=
absinC= sinC,
sinC,
∴ ab=
ab= ,即ab=
,即ab=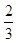 8分
8分
又a+b=2,在△ABC中,由余弦定理,
得cosC=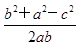 =
=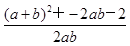 =
= , .10分
, .10分
又在△ABC中∠C∈(0,π),
∴∠C=60° .12分
考点:1. 正弦定理;2. 余弦定理.


科目:高中数学 来源: 题型:解答题
已知A、B、C为三角形ABC的三内角,其对应边分别为a,b,c,若有2acosC=2b+c成立.
(1)求A的大小;(2)若 ,
, ,求三角形ABC的面积.
,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设 (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函数关系式,并求函数的定义域;
的函数关系式,并求函数的定义域;
(2).如果 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 的位置应在哪里?如果
的位置应在哪里?如果 是参观线路,则希望它最长,
是参观线路,则希望它最长, 的位置又应在哪里?请予证明.
的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2, .
.
(1)若b=4,求sin A的值;
(2)若△ABC的面积S△ABC=4,求b,c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com