
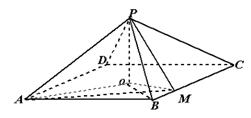
如图,四棱锥 中,底面是以
中,底面是以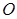 为中心的菱形,
为中心的菱形,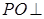 底面
底面 ,
,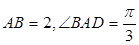 ,
,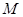 为
为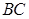 上一点,且
上一点,且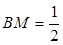 .
.
(1)证明: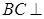 平面
平面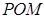 ;
;
(2)若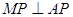 ,求四棱锥
,求四棱锥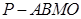 的体积.
的体积.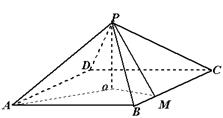
(1)详见解析;(2) .
.
解析试题分析:(1)因为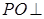 底面
底面 ,所以有
,所以有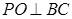 ,因此欲证
,因此欲证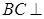 平面
平面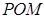 ,只要证
,只要证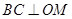 ,而这一点可通过连结
,而这一点可通过连结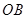 ,利用菱形的性质及勾股定理解决.
,利用菱形的性质及勾股定理解决.
(2)欲求四棱锥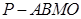 的体积.,必须先求出
的体积.,必须先求出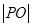 ,连结
,连结 ,设
,设 ,在
,在 利用余弦定理求出
利用余弦定理求出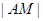 ,由三个直角三角形
,由三个直角三角形 ,依据勾股定理建立关于
,依据勾股定理建立关于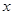 的方程即可.
的方程即可.
解:(1)如图,因 为菱形,
为菱形,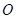 为菱形中心,连结
为菱形中心,连结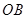 ,则
,则 ,因
,因 ,故
,故
又因为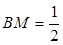 ,且
,且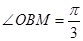 ,在
,在 中
中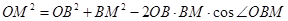
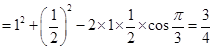
所以 ,故
,故
又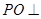 底面
底面 ,所以
,所以 ,从而
,从而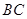 与平面
与平面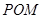 内两条相交直线
内两条相交直线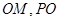 都垂直,所以
都垂直,所以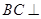 平面
平面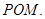
(2)解:由(1)可知,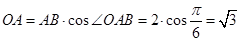
设 ,由
,由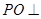 底面
底面 知,
知,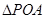 为直角三角形,故
为直角三角形,故
由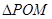 也是直角三角形,故
也是直角三角形,故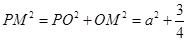
连结 ,在
,在 中,
中,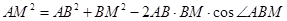

由已知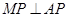 ,故
,故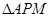 为直角三角形,则
为直角三角形,则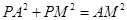
即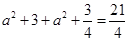 ,得
,得 ,
,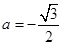 (舍去),即
(舍去),即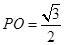
此时

所以四棱锥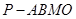 的体积
的体积
考点:1、直线与平面垂直的判定与性质;2、空间几何体的体积.3、余弦定理及勾股定理.


科目:高中数学 来源: 题型:解答题
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为 +2,且sinA+sinB=
+2,且sinA+sinB= sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为 sinC,求角C的度数.
sinC,求角C的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·郧阳模拟)设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)(a-b+c)=ac.
(1)求B.
(2)若sinAsinC= ,求C.
,求C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com