
分析 (1)把点A(1,0),B(2,-$\frac{1}{4}$)的坐标代入方程f(x)=ax+m,求解关于a,m的方程组得答案;
(2)由f(x)=$(\frac{1}{2})^{x}-\frac{1}{2}$在[-2,b]上为减函数求得函数的最值,再由最大值是最小值的7倍列式求得b的值;
(3)把不等式ln[(4-t)f(x)+$\frac{1}{2}$t]>0转化为(4-t)f(x)+$\frac{1}{2}$t>1,把f(x)代入,然后更换主元,令g(t)=$[1-(\frac{1}{2})^{x}]t+4•(\frac{1}{2})^{x}-3$,由$\left\{\begin{array}{l}{g(-1)=(\frac{1}{2})^{x}-1+4•(\frac{1}{2})^{x}-3>0}\\{g(1)=1-(\frac{1}{2})^{x}+4•(\frac{1}{2})^{x}-3>0}\end{array}\right.$,解不等式组求得实数x的取值范围.
解答 解:(1)∵函数f(x)=ax+m(a>0,且a≠1)的图象经过点A(1,0),B(2,-$\frac{1}{4}$),
∴$\left\{\begin{array}{l}{a+m=0}\\{{a}^{2}+m=-\frac{1}{4}}\end{array}\right.$,解得:a=$\frac{1}{2}$,m=-$\frac{1}{2}$;
(2)f(x)=$(\frac{1}{2})^{x}-\frac{1}{2}$,函数在[-2,b]上为减函数,则$f(x)_{min}=(\frac{1}{2})^{b}-\frac{1}{2}$,$f(x)_{max}=(\frac{1}{2})^{-2}-\frac{1}{2}=\frac{7}{2}$,
由题意可得$\frac{7}{2}=7((\frac{1}{2})^{b}-\frac{1}{2})$,即$(\frac{1}{2})^{b}=1$,解得b=0;
(3)不等式ln[(4-t)f(x)+$\frac{1}{2}$t]>0,即(4-t)f(x)+$\frac{1}{2}$t>1,
也就是(4-t)[$(\frac{1}{2})^{x}-\frac{1}{2}$]+$\frac{1}{2}t$>1,即$[1-(\frac{1}{2})^{x}]t+4•(\frac{1}{2})^{x}-3>0$.
则问题转化为对任意实数t∈[-1,1],不等式$[1-(\frac{1}{2})^{x}]t+4•(\frac{1}{2})^{x}-3>0$恒成立,求x得范围.
令g(t)=$[1-(\frac{1}{2})^{x}]t+4•(\frac{1}{2})^{x}-3$,则$\left\{\begin{array}{l}{g(-1)=(\frac{1}{2})^{x}-1+4•(\frac{1}{2})^{x}-3>0}\\{g(1)=1-(\frac{1}{2})^{x}+4•(\frac{1}{2})^{x}-3>0}\end{array}\right.$,
解得:$\frac{2}{3}<(\frac{1}{2})^{x}<\frac{4}{5}$,
∴$lo{g}_{\frac{1}{2}}\frac{4}{5}<x<lo{g}_{\frac{1}{2}}\frac{2}{3}$.
∴实数x的取值范围是($-lo{g}_{2}\frac{4}{5},-lo{g}_{2}\frac{2}{3}$).
点评 本题考查指数函数和对数函数的性质,考查了函数恒成立问题,考查了数学转化思想方法,训练了指数不等式和对数不等式的解法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$i | B. | $\frac{3}{5}$i | C. | i | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 | ||
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5次 | B. | 6次 | C. | 7次 | D. | 8次 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
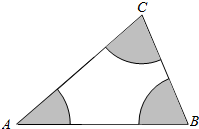 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com