
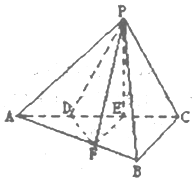
 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.分析 (1)由已知可得△PDE≌△PCE,得PE⊥DC,又平面PAC⊥平面ABC,可得PE⊥平面ABC,则PE⊥AB,再由AB⊥BC,EF∥BC,结合线面垂直的判定可得AB⊥平面PEF;
(2)求解直角三角形可得三角形ABC的面积,再由比例关系求得四边形BCEF的面积及三角形DEF的面积,可得四边形DFBC的面积,代入棱锥体积公式求得
四棱锥P-DFBC的体积.
解答 (1)证明:在△PDE与△PCE中,
∵PD=PC,DE=EC,PE=PE,∴△PDE≌△PCE,
则PE⊥DC,∵平面PAC⊥平面ABC,
且平面PAC∩平面ABC=AC,
∴PE⊥平面ABC,则PE⊥AB,
∵AB⊥BC,EF∥BC,∴AB⊥EF,又PE∩EF=E,
∴AB⊥平面PEF;
(2)解:∵AC=3,BC=$\sqrt{3}$,且∠ABC=$\frac{π}{2}$,
∴$AB=\sqrt{{3}^{2}-(\sqrt{3})^{2}}=\sqrt{6}$,
∴${S}_{△ABC}=\frac{1}{2}×\sqrt{6}×\sqrt{3}=\frac{3\sqrt{2}}{2}$,
∵AE:AC=2:3,∴S△AEF:S△ABC=4:9,
则${S}_{△AEF}=\frac{2\sqrt{2}}{3}$,∴${S}_{BCEF}=\frac{3\sqrt{2}}{2}-\frac{2\sqrt{2}}{3}=\frac{5\sqrt{2}}{6}$,
${S}_{△DEF}=\frac{1}{2}{S}_{△AFE}=\frac{\sqrt{2}}{6}$,
∴${S}_{DFBC}=\frac{5\sqrt{2}}{6}+\frac{\sqrt{2}}{6}=\sqrt{2}$.
∴${V}_{P-DFBC}=\frac{1}{3}×\sqrt{2}×\sqrt{3}=\frac{\sqrt{6}}{3}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
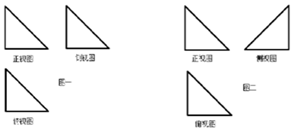 小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{6}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | ±$\sqrt{6}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
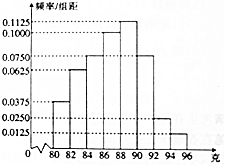 某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )
某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )| A. | 第3组 | B. | 第4组 | C. | 第5组 | D. | 第6组 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com