
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
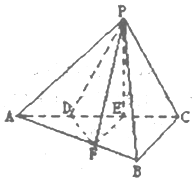 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
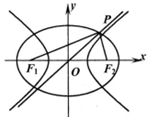 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 15 | C. | 45 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com