
分析 (1)由accosB-bccosA=3b2,利用余弦定理可得$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$-$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2}$=3b2,化简即可得出.
(2)由角C为锐角,sinC=$\frac{2\sqrt{2}}{3}$,可得cosC=$\sqrt{1-si{n}^{2}C}$.利用余弦定理可得$(\sqrt{11})^{2}$=a2+b2-2ab×$\frac{1}{3}$,与a=2b联立解得b,a,即可得出.
解答 解:(1)∵accosB-bccosA=3b2,
∴$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2}$-$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2}$=3b2,化为:a=2b,因此$\frac{a}{b}$=2.
(2)∵角C为锐角,sinC=$\frac{2\sqrt{2}}{3}$,∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{1}{3}$.
∴$(\sqrt{11})^{2}$=a2+b2-2ab×$\frac{1}{3}$,化为:3a2+3b2-2ab=33,又a=2b,
联立解得b2=3,∴S△ABC=$\frac{1}{2}ab$sinC=$\frac{1}{2}×2{b}^{2}sinC$=$3×\frac{2\sqrt{2}}{3}$=2$\sqrt{2}$.
点评 本题考查了余弦定理、同角三角函数基本关系式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{6}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | ±$\sqrt{6}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
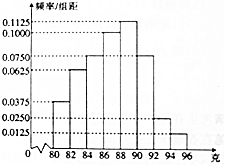 某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )
某仪器厂从新生产的一批零件中随机抽取40个检测,如图是根据抽样检测后零件的质量(单位:克)绘制的频率分布直方图,样本数据分8组,分别为[80,82),[82,84),[84,86),[86,88),[88,90),[90,92),[92,94),[94,96],则样本的中位数在( )| A. | 第3组 | B. | 第4组 | C. | 第5组 | D. | 第6组 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com