Question

12．△ABC外接圆的半径为1，圆心为O，$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow 0$，则$\overrightarrow{OC}•\overrightarrow{AB}$=-$\frac{1}{5}$．

Answer 1

分析 将已知等式移项，两边平方，得到$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，再将向量OC用向量OA，OB表示，代入所求式子，化简即可得到．

解答 解：∵$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow 0$，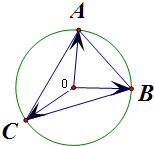
∴移项得3$\overrightarrow{OA}$+4$\overrightarrow{OB}$=-5$\overrightarrow{OC}$．
两边平方得，9${\overrightarrow{OA}}^{2}$+24$\overrightarrow{OA}$•$\overrightarrow{OB}$+16${\overrightarrow{OB}}^{2}$=25${\overrightarrow{OC}}^{2}$
∵O为△ABC的外接圆的圆心，
∴|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1，
上式化简为24$\overrightarrow{OA}$•$\overrightarrow{OB}$+=0，
∵$\overrightarrow{OC}$=-$\frac{1}{5}$（3$\overrightarrow{OA}$+4$\overrightarrow{OB}$），
∴$\overrightarrow{OC}•\overrightarrow{AB}$=-$\frac{1}{5}$（3$\overrightarrow{OA}$+4$\overrightarrow{OB}$）•（$\overrightarrow{OB}$-$\overrightarrow{OA}$）=-$\frac{1}{5}$（4${\overrightarrow{OB}}^{2}$-3${\overrightarrow{OA}}^{2}$-$\overrightarrow{OA}$•$\overrightarrow{OB}$）=-$\frac{1}{5}$，
故答案为：-$\frac{1}{5}$．

点评 本题考查向量的加减和数量积运算，考查向量的数量积的性质和平方法解题，属于中档题．