
分析 设BM=x,AC=h,利用两角和差的正切公式计算tan∠BAM,整理解得:h=$\sqrt{6}$x,即可计算解得sin∠MAC的值.
解答 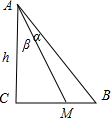 解:∵BC=$\frac{3}{2}$CM=(BM+MC),
解:∵BC=$\frac{3}{2}$CM=(BM+MC),
∴2BM=CM,
设∠BAM=α,∠CAM=β,BC=3BM=3x,AC=h.
∵tan∠BAM=$\frac{{\sqrt{6}}}{12}$,
又∵tanβ=$\frac{2x}{h}$,tan(α+β)=$\frac{3x}{h}$,
∴tanα=$\frac{\frac{3x}{h}-\frac{2x}{h}}{1+\frac{6{x}^{2}}{{h}^{2}}}$=$\frac{hx}{{h}^{2}+6{x}^{2}}$=$\frac{{\sqrt{6}}}{12}$,整理解得:h=$\sqrt{6}$x,
∴sin∠MAC=$\frac{2x}{\sqrt{4{x}^{2}+{h}^{2}}}$=$\frac{2x}{\sqrt{4{x}^{2}+6{x}^{2}}}$=$\frac{{\sqrt{10}}}{5}$.
故答案为:$\frac{{\sqrt{10}}}{5}$.
点评 本题考查了三角形中的几何运算,考查了数形结合思想和转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱柱ABC-A1B1C1所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.
如图,正三棱柱ABC-A1B1C1所有棱长都是2,D是棱AC的中点,E是棱CC1的中点,AE交A1D于点H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 0~6 | 7 | 8 | 9 | 10 |
| P | 0 | 0.2 | 0.3 | 0.3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?x∈R,{x^2}-x+\frac{1}{4}≥0$ | B. | ?x0∈R,sinx0≥1 | ||
| C. | ?x0∈R,sinx0+cosx0=2 | D. | $?x∈(0,\frac{π}{2}),x>sinx$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y'=-2sin(2x-1) | B. | y'=-2cos(2x-1) | C. | y'=-sin(2x-1) | D. | y'=-cos(2x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值8 | B. | 最大值6 | C. | 最大值4 | D. | 最大值2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com