
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,过动点
,过动点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() .记动点
.记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
①若![]() 为线段
为线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
②设![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 面积
面积![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)①
(2)①![]() .②
.②![]()
【解析】
(1)设![]() ,利用直接法求曲线的方程;
,利用直接法求曲线的方程;
(2)①由已知,分析可知直线![]() 的斜率存在且不为零,设
的斜率存在且不为零,设![]() ,联立抛物线方程,利用韦达定理解决;②将
,联立抛物线方程,利用韦达定理解决;②将![]() 用直线
用直线![]() 的斜率表示,即
的斜率表示,即![]() ,再结合
,再结合![]() 的范围即可解决.
的范围即可解决.
(1)设![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() .
.
所以曲线![]() 的方程为
的方程为![]() .
.
(2)①若直线![]() 的斜率不存在,则
的斜率不存在,则![]() 与曲线
与曲线![]() 无公共点,因此
无公共点,因此![]() 的斜率存在;
的斜率存在;
若![]() 的斜率为0,则
的斜率为0,则![]() 与曲线
与曲线![]() 只有一个公共点,因此
只有一个公共点,因此![]() 的斜率不为0.
的斜率不为0.
设![]() ,
,
由![]() 得
得![]() ,于是
,于是![]() ,解得
,解得![]() 且
且![]() .
.
设![]() ,
,![]() ,则
,则![]() .
.
因为![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,所以
,所以![]() ,
,
因此![]() ,所以
,所以![]() ,符合
,符合![]() 且
且![]() ,
,
于是![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() .
.
②因为点![]() ,
,![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
于是点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,
,
所以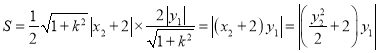 .
.
因为![]() ,所以
,所以![]() .
.
又因为![]() 且
且![]() ,因此
,因此![]() ,
,
即![]() 面积
面积![]() 的取值范围为
的取值范围为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足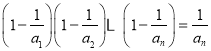 ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,若对于一切
,若对于一切![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 中存在某项
中存在某项![]() 满足
满足![]() 成等差数列?若存在,求出符合题意的
成等差数列?若存在,求出符合题意的![]() 的集合;若不存在,请说明理由.
的集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目:高中数学 来源: 题型:
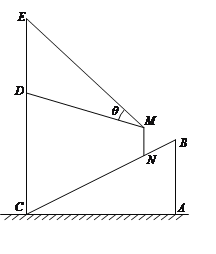
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高![]() 为
为![]() 米,它所占水平地面的长
米,它所占水平地面的长![]() 为
为![]() 米.该广告画最高点
米.该广告画最高点![]() 到地面的距离为
到地面的距离为![]() 米,最低点
米,最低点![]() 到地面距离
到地面距离![]() 米.假设某人眼睛到脚底的距离
米.假设某人眼睛到脚底的距离![]() 为
为![]() 米,他竖直站在此电梯上观看
米,他竖直站在此电梯上观看![]() 视角为
视角为![]() .
.
(Ⅰ)设此人到直线![]() 的距离为
的距离为![]() 米,试用含
米,试用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)此人到直线![]() 的距离为多少米时,视角
的距离为多少米时,视角![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
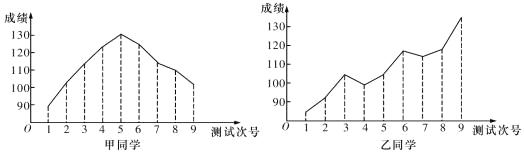
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间![]() 内;
内;
③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com