
| A. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 | |
| B. | 命题“存在x∈R,x2+x-l<0”的否定是“任意x∈R,x2+x-l>0”. | |
| C. | 线性回归方程y=$\hat bx$+a对应的直线一定经过其样本数据点(x1,y1)(x2,y2)、…,(xn,yn) 中的一个 | |
| D. | “b=0”是“函数f(X)=ax2+bx+c是偶函数”的充要条件” |
分析 由可导函数的极值点处的导数为0,导数为0的点不一定是极值点判断A;直接写出命题的否定判断B;由线性回归方程y=$\hat bx$+a对应的直线可能不经过其样本数据点(x1,y1)(x2,y2)、…,(xn,yn)中的任何一个判断C;利用偶函数的性质结合必要条件、充分条件及充分必要条件的判断方法判断D.
解答 解:若x0为函数f(x)极值点,则f′(x0)=0,反之,若f′(x0)=0,x0不一定为函数f(x)极值点,如f(x)=x3,故A错误;
命题“存在x∈R,x2+x-l<0”的否定是“任意x∈R,x2+x-l≥0”,故B错误;
线性回归方程y=$\hat bx$+a对应的直线可能不经过其样本数据点(x1,y1)(x2,y2)、…,(xn,yn)中的任何一个,故C错误;
若b=0,则函数f(x)=ax2+c是偶函数,反之,若函数f(x)=ax2+bx+c是偶函数,
则f(-x)-f(x)=ax2-bx+c-ax2-bx-c=0恒成立,即-2bx=0恒成立,∴b=0,即“b=0”是“函数f(X)=ax2+bx+c是偶函数”的充要条件”.
故选:D.
点评 本题考查必要条件、充分条件及充分必要条件的判断方法,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
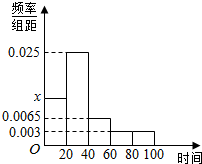 某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 7 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ;
; ;
; ;
; .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com