
分析 利用一元二次不等式的解法分别化简p,q可得解集A,B,p是q的必要不充分条件,可得B?A.
解答 解:由命题p:x2-8x-20>0,解得x<-2或x>10,设A={x|x<-2或x>10}.
q:x2-2x+1-m2>0(m>0),因式分解为:[x-(1-m)][x-(1+m)]>0,解得x<1-m,或x>1+m(m>0).
即命题q对应的集合为B={x|x<1-m,或x>1+m(m>0)}.
∵p是q的必要不充分条件,∴B?A.
故有$\left\{\begin{array}{l}m>0\\ 1-m≤-2\\ 1+m≥10\end{array}\right.$,解得m≥9.
即实数m的取值范围是[9,+∞).
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
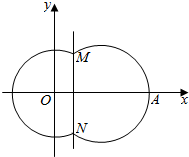 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{28}$ | B. | $-\frac{1}{56}$ | C. | $\frac{1}{28}$ | D. | $\frac{1}{56}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 | |
| B. | 命题“存在x∈R,x2+x-l<0”的否定是“任意x∈R,x2+x-l>0”. | |
| C. | 线性回归方程y=$\hat bx$+a对应的直线一定经过其样本数据点(x1,y1)(x2,y2)、…,(xn,yn) 中的一个 | |
| D. | “b=0”是“函数f(X)=ax2+bx+c是偶函数”的充要条件” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com