
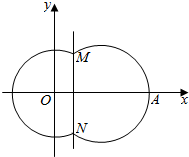
 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).分析 (1)根据圆弧 C1所在圆的方程为 x2+y2=169,可得M,N的坐标,从而可得直线AM的方程为 y-6=2(x-17),进而可求圆弧 C2所在圆的圆心为 (14,0),圆弧C2 所在圆的半径为=29-14=15,故可求圆弧C2 的方程;
(2)假设存在这样的点P(x,y),则由PA=$\sqrt{30}$PO,得x2+y2+2x-29=0,分别与圆弧方程联立,即可知这样的点P不存在.
解答 解:(1)圆弧 C1所在圆的方程为 x2+y2=169,令x=5,
解得M(5,12),N(5,-12)…2分
则直线AM的中垂线方程为 y-6=2(x-17),
令y=0,得圆弧 C2所在圆的圆心为 (14,0),
又圆弧C2 所在圆的半径为29-14=15,
所以圆弧C2 的方程为(x-14)2+y2=225(5≤x≤29)…5分
(2)假设存在这样的点P(x,y),则由PA=$\sqrt{30}$PO,得x2+y2+2x-29=0 …8分
由$\left\{\begin{array}{l}{x}^{2}+{y}^{2}+2x-29=0\\{x}^{2}+{y}^{2}=169\end{array}\right.$,解得x=-70 (舍去) 9分
由$\left\{\begin{array}{l}{x}^{2}+{y}^{2}+2x-29=0\\{(x-14)}^{2}+{y}^{2}=225\end{array}\right.$,解得 x=0(舍去),
综上知,这样的点P不存在…10分
点评 本题以圆为载体,考查圆的方程,考查曲线的交点,同时考查距离公式的运用,综合性强.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $({0,\frac{3}{2}})$ | C. | (1,2) | D. | $({1,\frac{3}{2}})∪({\frac{3}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
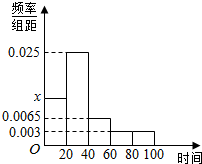 某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com