
分析 过点D作DE⊥AB于E,过点D作DF⊥BC于F,根据余弦定理可证得cosC=$\sqrt{3}$cosA-1,然后根据三角形的面积公式及sin2α+cos2α=1,将△ABD和△BCD的面积的平方和用cosA的表达式表示,然后运用配方法可得当cosA=$\frac{\sqrt{3}}{6}$时,△ABD和△BCD的面积的平方和最大,然后运用三角函数及勾股定理依次求出AE、BE、DE、BD的值,就可证到△ABD为等腰三角形.
解答 解:△ABD为等腰三角形.
理由如下:
过点D作DE⊥AB于E,过点D作DF⊥BC于F,如图,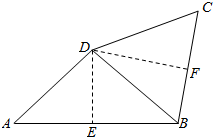 ,
,
则有DE=AD•sinA=10sinA,DF=DC•sinC=10sinC.
根据余弦定理可得:
DB2=AD2+AB2-2AD•AB•cosA=100+300-200$\sqrt{3}$cosA=400-200$\sqrt{3}$cosA,
DB2=DC2+BC2-2DC•BC•cosC=100+100-200cosC=200-200cosC,
∴400-200$\sqrt{3}$cosA=200-200cosC,
∴cosC=$\sqrt{3}$cosA-1.
∵AB=10$\sqrt{3}$,BC=CD=DA=10,
∴(S△ABD)2+(S△DBC)2=($\frac{1}{2}$AB•DE)2+($\frac{1}{2}$BC•DF)2
=($\frac{\sqrt{3}}{2}$•sinA•100)2+($\frac{1}{2}$sinC•100)2=100($\frac{3}{4}$sin2A+$\frac{1}{4}$sin2C).
=100[$\frac{3}{4}$(1-cos2A)+$\frac{1}{4}$(1-cos2C)]=100[1-$\frac{3}{4}$cos2A-$\frac{1}{4}$cos2C]
=100[1-$\frac{3}{4}$cos2A-$\frac{1}{4}$($\sqrt{3}$cosA-1)2]=100[-$\frac{3}{2}$cos2A+$\frac{\sqrt{3}}{2}$cosA+$\frac{3}{4}$
=-$\frac{3}{2}$(cos2A-$\frac{\sqrt{3}}{3}$cosA)+$\frac{3}{4}$=-$\frac{3}{2}$[(cosA-$\frac{\sqrt{3}}{6}$)2-$\frac{1}{12}$]+$\frac{3}{4}$]
=100[-$\frac{3}{2}$(cosA-$\frac{\sqrt{3}}{6}$)2+$\frac{7}{8}$]
∴当cosA=$\frac{\sqrt{3}}{6}$时,(S△ABD)2+(S△DBC)2取到最大值为$\frac{7}{8}$×100=$\frac{175}{2}$,
此时AE=AD•cosA=$\frac{\sqrt{3}}{6}$×10=$\frac{5\sqrt{3}}{3}$,BE=AB-AE=,
DE=$\sqrt{{AD}^{2}{-AE}^{2}}$=10$\sqrt{\frac{11}{12}}$,DB=$\sqrt{{DE}^{2}{+BE}^{2}}$=10$\sqrt{3}$,
∴DB=AB=10$\sqrt{3}$,
∴△ABD为等腰三角形.
点评 本题主要考查了余弦定理、三角函数、勾股定理、等腰三角形的判定等知识,还用到了公式sin2α+cos2α=1,运用配方法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定关于x轴对称 | B. | 一定关于y轴对称 | C. | 关于原点对称 | D. | 不具有对称性 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
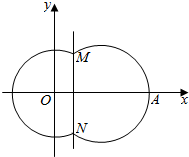 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com