
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
分析 利用数量积公式和二倍角公式化简f(x).
解答 解:∵向量$\overrightarrow a=(cosx-sinx,2cosx)$,$\overrightarrow b=(cosx+sinx,sinx)(x∈R)$,
则函数$f(x)={(\overrightarrow a•\overrightarrow b)^2}-1$=[(cosx-sinx)(cosx+sinx)+2sinxcosx]2-1=(cos2x-sin2x)2-1=1-2sin2xcos2x-1=-sin4x,
∴f(x)的周期为T=$\frac{2π}{4}$=$\frac{π}{2}$.
∵f(-x)=-sin(-4x)=sin4x=-f(x),
∴f(x)是奇函数.
故选:D.
点评 本题考查了平面向量的数量积运算,三角函数的恒等变换,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | -2 | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
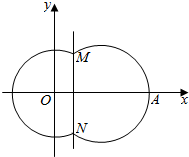 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com