
分析 (1)根据|x+1|+|x-2|≥|(x+1)-(x-2)|=3,求出f(x)的最小值;
(2)讨论x的取值范围,求出f(x)的解析式,再求不等式f(x)>4的解集.
解答 解:(1)因为|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
当且仅当-1≤x≤2时,等号成立,
所以f(x)的最小值等于3,即a=3;
(2)由(1)知,当-1≤x≤2时,f(x)=3,f(x)>4不成立;
当x<-1时,f(x)=-(x+1)-(x-2)=-2x+1,
不等式f(x)>4化为-2x+1>4,解得x<-$\frac{3}{2}$;
当x>2时,f(x)=(x+1)+(x-2)=2x-1,
不等式f(x)>4化为2x-1>4,解得x>$\frac{5}{2}$;
所以,不等式f(x)>4的解集为{x|x<-$\frac{3}{2}$或x>$\frac{5}{2}$}.
点评 本题考查了不等式的解法与应用问题,也考查了绝对值不等式的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | $({0,\frac{3}{2}})$ | C. | (1,2) | D. | $({1,\frac{3}{2}})∪({\frac{3}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
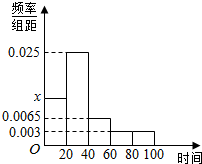 某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
某学校随机调查了部分学生的上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com