
(本题满分14分)在单调递增数列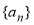 中,
中,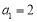 ,
,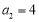 ,且
,且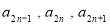 成等差数列,
成等差数列,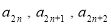 成等比数列,
成等比数列,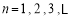 .
.
(Ⅰ)(ⅰ)求证:数列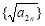 为等差数列;
为等差数列;
(ⅱ)求数列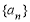 的通项公式.
的通项公式.
(Ⅱ)设数列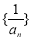 的前
的前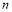 项和为
项和为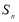 ,证明:
,证明: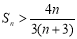 ,
,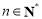 .
.
(1)紧扣等差数列定义证明,(2)当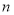 为偶数时
为偶数时
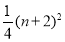 ,当
,当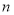 为奇数时
为奇数时
 .(3)证明见解析
.(3)证明见解析
【解析】
试题分析:要证明数列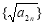 为等差数列,只需证明
为等差数列,只需证明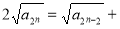
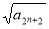 成立,由于数列首项为正,
成立,由于数列首项为正,
数列为单调递增,说以 ,由
,由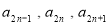 成等差数列,得
成等差数列,得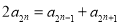 ……(1),由因为
……(1),由因为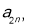
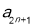 ,
,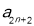 成等比数列,则
成等比数列,则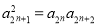 ,
,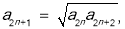 于是
于是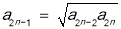 代入(1)式整理得:
代入(1)式整理得: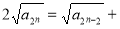
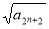 得证;先求
得证;先求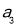 ,
,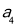 备用,由于数列
备用,由于数列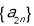 为等差数列,可借助等差数列通项公式求出
为等差数列,可借助等差数列通项公式求出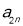 ,再由
,再由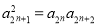 求出
求出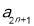 ,最后分
,最后分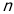 为奇数和偶数两种情况表达
为奇数和偶数两种情况表达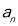 ,由于数列的通项公式分
,由于数列的通项公式分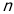 为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是
为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是
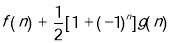 ,合成后对
,合成后对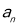 进行放缩,这里技巧很重要,
进行放缩,这里技巧很重要,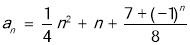
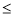
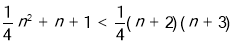 ,再求
,再求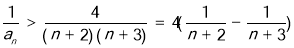 ,最后利用裂项相消法求和达到证明不等式的目的;
,最后利用裂项相消法求和达到证明不等式的目的;
试题解析:(ⅰ)因为数列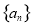 为单调递增数列,
为单调递增数列,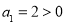 ,所以
,所以 (
(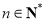 ).由题意
).由题意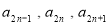
成等差数列,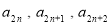 成等比数列,
成等比数列, .得
.得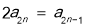
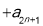 ,
,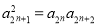 ,于是
,于是
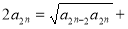
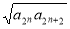 ,化简得
,化简得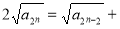
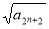 ,所以数列
,所以数列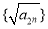 为等差数列.
为等差数列.
(ⅱ)又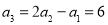 ,
,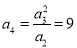 ,所以数列
,所以数列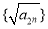 的首项为
的首项为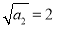 ,公差为
,公差为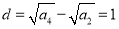 ,所以
,所以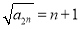 ,从而
,从而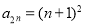 .结合
.结合 可得
可得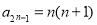 .因此,当
.因此,当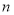 为偶数时
为偶数时
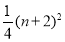 ,当
,当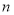 为奇数时
为奇数时
 .
.
(2)所以数列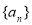 的通项公式为:
的通项公式为:
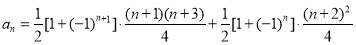
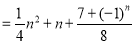 .因为
.因为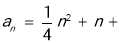
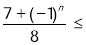
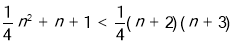 ,所以
,所以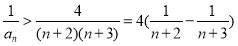 ;则有
;则有
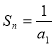
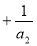
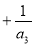
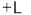
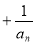
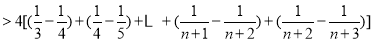
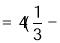
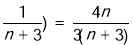 ,所以
,所以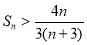 ,
,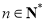 .
.
考点:数列与不等式


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源:2014-2015学年北京市丰台区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
已知数列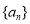 满足
满足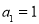 ,
,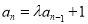 ,
,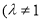 ,
,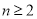 且
且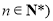 .
.
(1)求证:当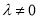 时,数列
时,数列 为等比数列;
为等比数列;
(2)如果 ,求数列
,求数列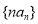 的前
的前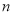 项和
项和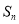 ;
;
(3)如果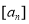 表示不超过
表示不超过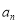 的最大整数,当
的最大整数,当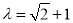 时,求数列
时,求数列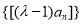 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高三三月阶段测试理科数学试卷(解析版) 题型:选择题
已知函数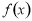 为R上的奇函数,当
为R上的奇函数,当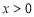 时,
时,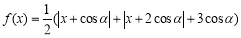
(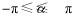 ),若对任意实数
),若对任意实数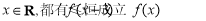 ,则实数
,则实数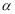 的取值范围是
的取值范围是
A. B.
B.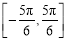 C.
C.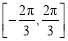 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知等差数列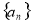 中,
中,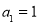 ,其前
,其前 项和
项和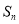 满足
满足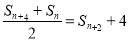 (
(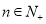 ).
).
(1)求数列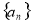 的通项公式;
的通项公式;
(2)令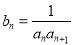 ,求数列
,求数列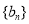 的前
的前 项和
项和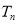 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com