
已知数列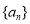 满足
满足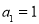 ,
,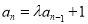 ,
,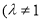 ,
,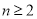 且
且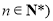 .
.
(1)求证:当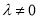 时,数列
时,数列 为等比数列;
为等比数列;
(2)如果 ,求数列
,求数列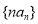 的前
的前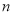 项和
项和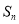 ;
;
(3)如果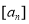 表示不超过
表示不超过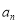 的最大整数,当
的最大整数,当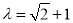 时,求数列
时,求数列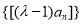 的通项公式.
的通项公式.
科目:高中数学 来源: 题型:
光线自点M(2,3)射到N(1,0)后被x轴反射,则反射光线所在的直线方程为( )
A.y=3x-3 B.y=-3x+3
C.y=-3x-3 D.y=3x+3
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市石景山区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
以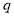 为公比的等比数列
为公比的等比数列 中,
中,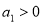 ,则“
,则“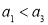 ”是“
”是“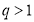 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市丰台区高三上学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数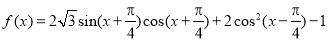 ,
,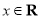 .
.
(1)求函数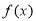 的最小正周期;
的最小正周期;
(2)求函数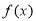 在区间
在区间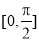 上的最大值和最小值及相应的x的值.
上的最大值和最小值及相应的x的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市丰台区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是
(A){1,3} (B){0,1,3}
(C){0,1,3,4} (D){0,1,2,3,4}
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省深圳市高三第一次调研考试文科数学试卷(解析版) 题型:选择题
如图,三棱锥A-BCD中,AB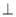 平面BCD,BC
平面BCD,BC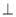 CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为( )
CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为( )
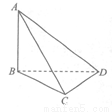
A.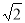 B.2 C.
B.2 C.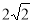 D.
D.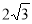
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高三三月阶段测试理科数学试卷(解析版) 题型:解答题
(本题满分14分)在单调递增数列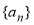 中,
中,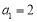 ,
,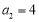 ,且
,且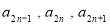 成等差数列,
成等差数列,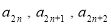 成等比数列,
成等比数列,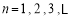 .
.
(Ⅰ)(ⅰ)求证:数列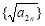 为等差数列;
为等差数列;
(ⅱ)求数列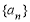 的通项公式.
的通项公式.
(Ⅱ)设数列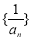 的前
的前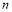 项和为
项和为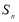 ,证明:
,证明: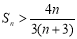 ,
,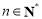 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com