
(2011•宁德模拟)将双曲线x2﹣y2=2绕原点逆时针旋转45°后可得到双曲线y= .据此类推可求得双曲线
.据此类推可求得双曲线 的焦距为( )
的焦距为( )
A.2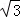 B.2
B.2 C.4 D.4
C.4 D.4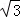
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:填空题
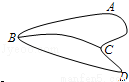
(2009•浦东新区二模)某赛车场的路线中有A,B,C,D四个维修站如图所示.若维修站之间有路线直接连接(不经过其它维修站),则记为1;若没有直接路线连接,则记为0(A与A,B与B,C与C,D与D记0),现用矩阵表示这些维修站间路线连接情况为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:选择题
(2014•遵义二模)定义行列式运算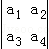 =a1a4﹣a2a3.将函数
=a1a4﹣a2a3.将函数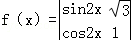 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是( )
个单位,以下是所得函数图象的一个对称中心是( )
A. B.
B.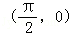 C.
C. D.
D.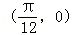
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在平面直角坐标系中O为坐标原点,P(3,4),将向量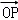 绕原点顺时针方向旋转
绕原点顺时针方向旋转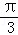 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量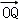 ,则点Q的坐标是( )
,则点Q的坐标是( )
A.(3+4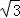 ,4﹣3
,4﹣3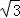 ) B.(4+3
) B.(4+3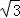 ,4﹣3
,4﹣3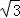 )
)
C.(3+4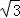 ,3
,3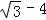 ) D.(3﹣4
) D.(3﹣4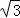 ,3﹣4
,3﹣4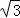 )
)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在同一平面直角坐标系中,将曲线y=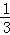 cos2x按伸缩变换
cos2x按伸缩变换 变换为( )
变换为( )
A.y′=cosx′ B.y′=3cos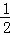 ′ C.y′=2cos
′ C.y′=2cos x′ D.y′=
x′ D.y′=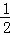 cos3x′
cos3x′
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:填空题
(2007•茂名二模)已知圆柱半径是2,则是一个与圆柱的轴成45°角的平面截圆柱面所得截痕曲线的离心率是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
一平面截球面产生的截面形状是 ;它截圆柱面所产生的截面形状是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
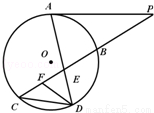
(2014•天津一模)如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:选择题
A、B、C是⊙O上三点,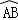 的度数是50°,∠OBC=40°,则∠OAC等于( )
的度数是50°,∠OBC=40°,则∠OAC等于( )
A.15°或65° B.25° C.30° D.15°或40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com