
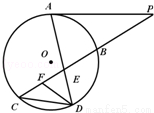
(2014•天津一模)如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA= .
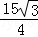
【解析】
试题分析:利用△DEF∽△CED与已知可得EC的长,进而得到BE,利用相交弦定理可得AE•ED=EB•CE,得到AE.再利用AP∥CD,可得△AEP∽△FED,得到PE,进而得到PB,再利用切割线定理可得PA2=PB•PC即可得出.
【解析】
在△DEF和△CED中,∵∠EDF=∠C,∠DEF公用,∴△DEF∽△CED,∴ ,
,
∵DE=3,EF=2,∴EC= =
= .
.
∵CE:BE=3:2,∴BE=3.
由相交弦定理可得AE•ED=EB•CE,∴AE= =
=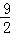 .
.
∵AP∥CD,∴∠P=∠C,
∴∠P=∠EDF.
∴△AEP∽△FED,∴ ,
,
∴ =
= =
=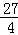 .
.
∴PB=PE﹣EB= .
.
∵PA与⊙O相切,∴PA2=PB•PC=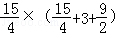 =
= .
.
∴PA=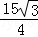 .
.
故答案为: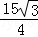 .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
(2011•宁德模拟)将双曲线x2﹣y2=2绕原点逆时针旋转45°后可得到双曲线y= .据此类推可求得双曲线
.据此类推可求得双曲线 的焦距为( )
的焦距为( )
A.2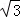 B.2
B.2 C.4 D.4
C.4 D.4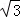
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:选择题
工人师傅在如图1的一块矩形铁皮上画一条曲线,沿曲线剪开,将所得到的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.工人师傅所画的曲线是( )
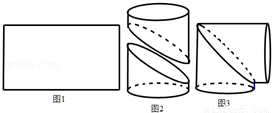
A.一段圆弧 B.一段抛物线 C.一段双曲线 D.一段正弦曲线
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
(2013•东莞一模)(几何证明选讲选做题)
如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则线段DO的长等于 .
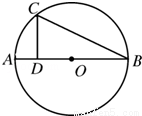
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
(2014•黄冈模拟)已在点C在圆O的直径BE的延长线上,直线CA与圆O相切于点A,∠ACB的平分线分别交AB、AE于点D、F,则∠ADF= .
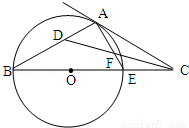
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图,⊙O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )

A.40° B.55° C.65° D.70°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
(2010•石景山区一模)如图,已知PE是圆O的切线.直线PB交圆O于A、B两点,PA=4,AB=12, .则PE的长为 ,∠ABE的大小为 °.
.则PE的长为 ,∠ABE的大小为 °.
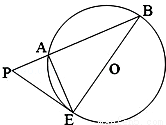
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•陕西模拟)已知[x]表示不超过实数x的最大整数(x∈R),如:[﹣1,3]=﹣2,[0.8]=0,[3,4]=3.定义{x}=x﹣[x],求{ }+{
}+{ }+{
}+{ }+…+{
}+…+{ }=( )
}=( )
A.2013 B. C.1007 D.2014
C.1007 D.2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com