
(2014•黄冈模拟)已在点C在圆O的直径BE的延长线上,直线CA与圆O相切于点A,∠ACB的平分线分别交AB、AE于点D、F,则∠ADF= .
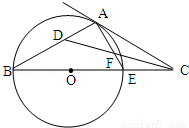
45°
【解析】
试题分析:因为AC为圆O的切线,由弦切角定理,则∠B=∠EAC.又CD平分∠ACB,则∠ACD=∠BCD,两式相加,∠B+∠BCD=∠EAC+∠ACD,根据三角形外角定理,∠ADF=∠AFD,又∠BAE=90°,,△ADF是等腰直角三角形,所以∠ADF=∠AFD=45°.
【解析】
因为AC为圆O的切线,由弦切角定理,则∠B=∠EAC.
又CD平分∠ACB,则∠ACD=∠BCD.
所以∠B+∠BCD=∠EAC+∠ACD.
根据三角形外角定理,∠ADF=∠AFD,
因为BE是圆O的直径,则∠BAE=90°,△ADF是等腰直角三角形,
所以∠ADF=∠AFD=45°.
故答案为:45°


 习题精选系列答案
习题精选系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:选择题
定义运算 ,如
,如 ,已知α+β=π,
,已知α+β=π,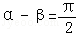 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:填空题
(2007•茂名二模)已知圆柱半径是2,则是一个与圆柱的轴成45°角的平面截圆柱面所得截痕曲线的离心率是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
给出下列四个命题:
①设x1,x2∈R,则x1>1且x2>1的充要条件是x1+x2>2且x1x2>1;
②任意的锐角三角形ABC中,有sinA>cosB成立;
③平面上n个圆最多将平面分成2n2﹣4n+4个部分;
④空间中直角在一个平面上的正投影可以是钝角.
其中真命题的序号是 (要求写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
(2014•天津一模)如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA= .
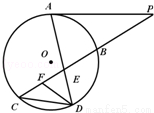
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图,经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P,若∠CAP=40°,∠ACP=100°,则
∠BAC所对的弧的度数为( )
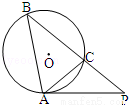
A.40° B.100° C.120° D.30°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=( )
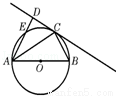
A.15° B.30° C.45° D.60°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
(2013•惠州二模)(几何证明选讲选做题)
如图所示,AB是圆O的直径, ,AB=10,BD=8,则cos∠BCE= .
,AB=10,BD=8,则cos∠BCE= .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•天津一模)定义一种新运算:a?b=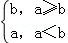 ,已知函数f(x)=(1+
,已知函数f(x)=(1+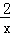 )?3log2(x+1),若方程f(x)﹣k=0恰有两个不相等的实根,则实数k的取值范围为( )
)?3log2(x+1),若方程f(x)﹣k=0恰有两个不相等的实根,则实数k的取值范围为( )
A.(﹣∞,3)
B.(1,3)
C.(﹣∞,﹣3)∪(1,3)
D.(﹣∞,﹣3)∪(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com