科目：高中数学 来源： 题型：
如图(6)，四棱锥S—ABCD的底面是正方形，侧棱SA⊥底面ABCD，
过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面
AEH交SC于K点，且AB=1，SA=2．
（1）设点P是SA上任一点，试求
的最小值；
（2）求证：E、H在以AK为直径的圆上；
（3）求平面AEKH与平面ABCD所成的锐二面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
在两个变量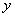
与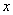
的回归模型中，分别选择了4个不同模型，它们的相关指数
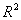如下，其中拟合效果最好的模型是（ ）
A． 模型1的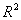为0．55 B．模型2的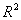为0．65
C． 模型3的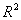为0．79 D．模型4的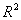为0．95
查看答案和解析>>
科目：高中数学 来源： 题型：
一个社会调查机构为了解某社区居民的月收入情况，从该社区成人居民中抽取10000人进行调查，根据所得信息制作了如图所示的样本频率分布直方图．
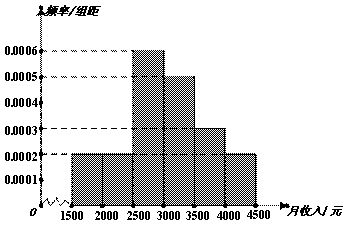（Ⅰ）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，试求其中月收入在[2000，2500）(2000元至2500元之间)的人数；
（Ⅱ）为了估计从该社区任意抽取的3个居民中恰有2人月收入在[2000，3000）的概率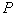
，特设计如下随机模拟的方法：先由计算器产生0到9之间取整数值的随机数，依次用0，1，2，3，…9的前若干个数字表示月收入在[2000，3000）的居民，剩余的数字表示月收入不在[2000，3000）的居民；再以每三个随机数为一组，代表收入的情况．
假设用上述随机模拟方法已产生了表中的20组随机数，请根据这批随机数估计概率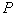的值．
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
（Ⅲ）任意抽取该社区的5位居民，用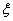
表示月收入在[2000，3000）（元）的人数，求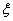的数学期望与方差．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)=x3+x,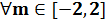
，f(mx-2)+f(x)<0恒成立，则x的取值范围为
A、（-2，
） B、（，2） C、（-2，2） D、（-3，2）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
Ｄ．
中，
为锐角，角
所对的边分别为
，且
的值；（II）若
，求
的值。 
