
一个社会调查机构为了解某社区居民的月收入情况,从该社区成人居民中抽取10000人进行调查,根据所得信息制作了如图所示的样本频率分布直方图.
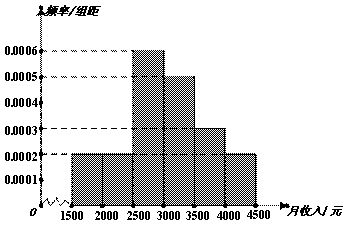 (Ⅰ)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,试求其中月收入在[2000,2500)(2000元至2500元之间)的人数;
(Ⅰ)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,试求其中月收入在[2000,2500)(2000元至2500元之间)的人数;
(Ⅱ)为了估计从该社区任意抽取的3个居民中恰有2人月收入在[2000,3000)的概率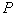 ,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示月收入在[2000,3000)的居民,剩余的数字表示月收入不在[2000,3000)的居民;再以每三个随机数为一组,代表收入的情况.
,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示月收入在[2000,3000)的居民,剩余的数字表示月收入不在[2000,3000)的居民;再以每三个随机数为一组,代表收入的情况.
假设用上述随机模拟方法已产生了表中的20组随机数,请根据这批随机数估计概率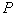 的值.
的值.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
(Ⅲ)任意抽取该社区的5位居民,用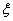 表示月收入在[2000,3000)(元)的人数,求
表示月收入在[2000,3000)(元)的人数,求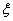 的数学期望与方差.
的数学期望与方差.
解:(Ⅰ)由频率分布直方图可知,月收入在[2000,2500)的频率为0.0002×500=0.1,所以应抽取的人数为0.1×100=10人
(Ⅱ)由频率分布直方图可知,月收入在[2000,3000)的频率为0.0002×500+0.0006×500=0.4
所以可以用数字0,1,2,3表示收入在[2000,3000)的居民,数字4,5,6,7,8,9表示月收入不在[2000,3000)的居民;
观察上述随机数可得,该社区3个居民中恰有2个月收入在[2000,3000)的有191,271,932,812,431,393,027,730,共有8个.
而基本事件一共有20个,根据古典概型的定义可知该社区3个居民中恰有2个月收入在[2000,3000)的概率为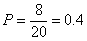
(Ⅲ)由频率分布直方图可知,任意抽取该社区1位居民,月收入在[2000,3000)(元)的概率为0.4,
所以随机变量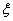 服从
服从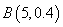 ,所以
,所以 ,
,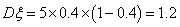


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
已知异面直线a,b所成的角为θ,P为空间任意一点,过P作直线l,若l与a,b所成的角均为 ,有以下命题:
,有以下命题:
①若θ= 60°, = 90°,则满足条件的直线l有且仅有l条;
= 90°,则满足条件的直线l有且仅有l条;
②若θ= 60°, =30°,则满足条件的直线l有仅有l条;
=30°,则满足条件的直线l有仅有l条;
③若θ= 60°, = 70°,则满足条件的直线l有且仅有4条;
= 70°,则满足条件的直线l有且仅有4条;
④若θ= 60°, = 45°,则满足条件的直线l有且仅有2条;
= 45°,则满足条件的直线l有且仅有2条;
上述4个命题中真命题有
A.l个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,,已知直线l的参数方程为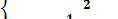 (t 为参数),曲线C的极坐标方程为
(t 为参数),曲线C的极坐标方程为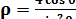 。
。
(1)求曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A、B两点,求│AB│的值、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com