
分析 (Ⅰ)利用奇函数的定义,即可得出结论;
(Ⅱ)由$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}=\frac{1}{2}$,得2x=3,x=log23,即可得出结论.
解答 解:(Ⅰ)因为函数f(x)的定义域为R,且$f(-x)=\frac{{{2^{-x}}-1}}{{{2^{-x}}+1}}=\frac{{1-{2^x}}}{{1+{2^x}}}=-f(x)$,
所以f(x)是定义在R上的奇函数; …(4分)
(Ⅱ)∵$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}=\frac{1}{2}$,∴2x=3,x=log23.
所以方程的实数解为x=log23.…(8分)
点评 本题考查函数的性质,考查方程思想,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{10}$+y2=1 | B. | $\frac{{x}^{2}}{19}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
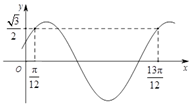 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,$φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2}$,$φ=\frac{π}{6}$ | C. | ω=2,$φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2}$,$φ=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
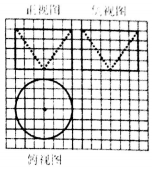 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )| A. | 39π | B. | 48π | C. | 57π | D. | 63π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 30° | C. | 90° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com