
分析 (Ⅰ)输出B的坐标,带入椭圆的方程,求出a2,b2的值,求出椭圆方程即可;
(Ⅱ)设直线PQ的方程为x=my+1,P(x1,y1),Q(x2,y2),联立方程组,得到(3m2+4)y2+6my-9=0,表示出$\frac{{|{TF}|}}{{|{PQ}|}}$,求出其范围即可.
解答 解:(Ⅰ)由y2=4x得其交点坐标是F(1,0),
设B(x0,y0),(x0>0,y0>0),
则|BF|=x0+1=$\frac{5}{3}$,解得:x0=$\frac{2}{3}$,
∴${{y}_{0}}^{2}$=4×$\frac{2}{3}$=$\frac{8}{3}$,
由点B在椭圆C上,得$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,
即$\frac{4}{{9a}^{2}}$+$\frac{8}{{3b}^{2}}$=1,又a2=b2+1,
解得:a2=4,b2=3,
∴椭圆C的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)设直线PQ的方程为x=my+1,P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3m2+4)y2+6my-9=0,
则△=36m2+36(3m2+4)>0,
y1+y2=$\frac{-6m}{{3m}^{2}+4}$,y1y2=$\frac{-9}{{3m}^{2}+4}$,
∴|PQ|=$\sqrt{1{+m}^{2}}$|y1-y2|=$\sqrt{1{+m}^{2}}$$\sqrt{{(\frac{-6m}{{3m}^{2}+4})}^{2}-4•\frac{-9}{{3m}^{2}+4}}$=$\frac{12{(m}^{2}+1)}{{3m}^{2}+4}$,
当m≠0时,直线FT的方程为y=-m(x-1),
由$\left\{\begin{array}{l}{x=4}\\{y=-m(x-1)}\end{array}\right.$,得x=4,y=-3m,
即T(4,-3m),
∴|TF|=3$\sqrt{1{+m}^{2}}$,
∴$\frac{|TF|}{|PQ|}$=$\frac{3\sqrt{1{+m}^{2}}}{1{+m}^{2}}$•$\frac{{3m}^{2}+4}{12}$=$\frac{1}{4}$(3$\sqrt{{m}^{2}+1}$+$\frac{1}{\sqrt{{m}^{2}+1}}$),
设t=$\sqrt{{m}^{2}=1}$,则t>1,
则$\frac{|TF|}{|PQ|}$=$\frac{3}{4}$t+$\frac{1}{4t}$,
应用y=$\frac{3}{4}$t+$\frac{1}{4t}$在(1,+∞)递增,
∴y>3+1=4,
则$\frac{|TF|}{|PQ|}$>$\frac{1}{4}$×4=1,
当m=0时,PQ的中点是F,T(4,0),
ze|TF|=3,|PQ|=$\frac{{2b}^{2}}{a}$=3,
∴$\frac{|TF|}{|PQ|}$=1,
综上,$\frac{{|{TF}|}}{{|{PQ}|}}$≥1,
故$\frac{{|{TF}|}}{{|{PQ}|}}$的取值范围是[1,+∞).
点评 本题考查了求椭圆的方程问题,考查直线和圆的位置关系以及不等式的应用,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
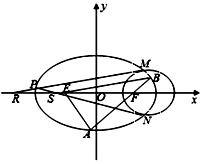 已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$
已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
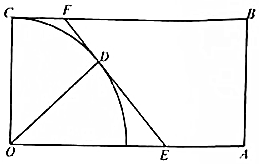 如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.
如图,矩形公园OABC中,OA=2km,OC=1km,公园的左下角阴影部分为以O为圆心,半径为1km的$\frac{1}{4}$圆面的人工湖,现计划修建一条与圆相切的观光道路EF(点E、F分别在边OA与BC上),D为切点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{{3{e^2}}},\frac{1}{e})$ | B. | $[\frac{2}{{3{e^2}}},\frac{1}{e})$ | C. | $(\frac{2}{{3{e^2}}},\frac{1}{2e})$ | D. | $[\frac{2}{{3{e^2}}},\frac{1}{2e})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com