
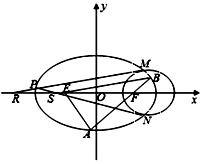
 已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$
已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3)的左右焦点分别为E,F,过点F作直线交椭圆C于A,B两点,若$\overrightarrow{AF}=2\overrightarrow{FB}$且$\overrightarrow{AE}•\overrightarrow{AB}=0$分析 (1)设|BF|=m,推导出(6-2m)2+(3m)2=(6-m)2,从而m=1,进而AE⊥AF.由此能求出椭圆C的方程.
(2)由条件可知M、N两点关于x轴对称,设M(x1,y1),P(x0,y0),则N(x1,-y1),直线PM的方程为$y-{y_0}=\frac{{{y_1}-{y_0}}}{{{x_1}-{x_0}}}(x-{x_0})$,令y=0得点R的横坐标${x_R}=\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}}$,同理可得点S的横坐标${x_S}=\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}$.由此能证明|OR|•|OS|为常数.
解答 解:(1)设|BF|=m,则|AF|=2m,|BE|=6-m,|AE|=6-2m,|AB|=3m.
则有(6-2m)2+(3m)2=(6-m)2,解得m=1,…3(分)
∴|AF|=2,|BE|=5,|AE|=4,|AB|=3,
∴|AB|2+|AE|2=|BE|2,∴AE⊥AF.
于是,在Rt△AEF中,|EF|2=|AE|2+|AF|2=42+22=20,
所以|EF|=2$\sqrt{5}$,所以b2=9-($\sqrt{5}$)2=4,
椭圆C的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1$.…6(分)
证明:(2)由条件可知M、N两点关于x轴对称,
设M(x1,y1),P(x0,y0),则N(x1,-y1),
$\frac{{{x}_{1}}^{2}}{9}+\frac{{{y}_{1}}^{2}}{4}$=1,$\frac{x_0^2}{9}+\frac{y_0^2}{4}=1$,
所以$x_1^2=\frac{9}{4}(4-y_1^2)$,$x_0^2=\frac{9}{4}(4-y_0^2)$.
直线PM的方程为$y-{y_0}=\frac{{{y_1}-{y_0}}}{{{x_1}-{x_0}}}(x-{x_0})$,…9(分)
令y=0得点R的横坐标${x_R}=\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}}$,
同理可得点S的横坐标${x_S}=\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}$.
于是$|{OR}|•|{OS}|=|{\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}}•\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}}|=|{\frac{x_1^2y_0^2-x_0^2y_1^2}{y_0^2-y_1^2}}|$
=$|{\frac{1}{y_0^2-y_1^2}•[\frac{9}{4}(4-y_1^2)y_0^2-\frac{9}{4}(4-y_0^2)y_1^2]}|=|{\frac{1}{y_0^2-y_1^2}•9(y_0^2-y_1^2)}|=9$,
所以,|OR|•|OS|为常数9.…12(分)
点评 本题考查椭圆方程的求法,考查两线段乘积为定值的证明,是中档题,解题时要认真审题,注意椭圆、韦达定理、直线性质的合理运用.


科目:高中数学 来源: 题型:选择题
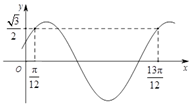 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | ω=2,$φ=\frac{π}{6}$ | B. | $ω=\frac{1}{2}$,$φ=\frac{π}{6}$ | C. | ω=2,$φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2}$,$φ=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
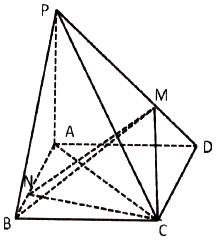 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,且PA=AB=AC=2,$BC=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.
已知抛物线E:y2=2px(p>0)的焦点过为F,过F且倾斜角为$\frac{π}{4}$的直线l被E截得的线段长为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}i$ | B. | $-\frac{5}{2}$ | C. | $-\frac{1}{2}i$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com