
思路分析:设P(x1,y1)、Q(x2,y2).由OP⊥OQx1x2+y1y2=0.
由方程组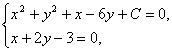 解得x1、x2、y1、y2.代入上式即可求C.
解得x1、x2、y1、y2.代入上式即可求C.
解法一:如图.设P(x1,y1)、Q(x2,y2).
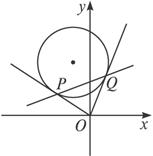
∵OP⊥OQ,
∴kOP·kOQ=-1.
∴x1x2+y2y2=0. ①
由方程组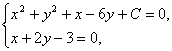 消去x得到5y2-20y+12+C=0,
消去x得到5y2-20y+12+C=0,
∴y1+y2=4,y1y2=![]() .
.
∴x1x2=(3-2y1)(3-2y2)=9-6(y1+y2)+4y1y2.
∴x1x2+y1y2=5y1y2-6(y1+y2)+9=0,
即12+C-6×4+9=0,解得C=3.
解法二:∵OP⊥OQ,
∴O、P、Q三点共圆,PQ是直径.
故以PQ为直径的圆的圆心为(m,n),方程为(x-m)2+(y-n)2=m2+n2.
PQ为两圆的公共弦.两圆相减得PQ方程为(1+2m)x+(-6+2n)y+C=0,它与直线x+2y-3=0是同一直线,
∴![]() ,m=-
,m=-![]() ,n=-
,n=-![]() .
.
∵圆心(m,n)在直线x+2y-3=0上,
∴-![]() -3=0.
-3=0.
∴C=3.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源:2002年高中会考数学必备一本全2002年1月第1版 题型:013
已知O为坐标原点,圆 =4与直线y=Kx交于P、Q两点,则|OP|·|OQ|的值是
=4与直线y=Kx交于P、Q两点,则|OP|·|OQ|的值是
[ ]

 +1
+1查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省示范高中高三(上)摸底数学试卷(文科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com