
分析 (1)计算向量的数量积,利用二倍角.两角和的正弦函数化简函数f(x)的表达式,得到一个角的一个三角函数的形式;借助正弦函数的最值,求出函数f(x)在$[{0,\frac{2π}{3}})$上的最值;
(2)由f(A)=sin(2A-$\frac{π}{6}$)=1,又A为锐角,即可解得A,从而由正弦定理解得C=$\frac{π}{2}$,可得△ABC为Rt△,即可求得b,由三角形面积公式即可得解.
解答 解:(1)$f(x)=({\vec a+\vec b})•\vec a-2={\vec a^2}+\vec a•\vec b-2$
=${sin^2}x+1+\sqrt{3}sinxcosx+\frac{1}{2}-2$
=$\frac{1-cos2x}{2}+\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}$
=$\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x$=$sin({2x-\frac{π}{6}})$.
当$x∈[{0,\frac{2π}{3}})$时,$2x-\frac{π}{6}∈[{-\frac{π}{6},\frac{7π}{6}})$,
结合正弦函数的图象知,当$2x-\frac{π}{6}=-\frac{π}{6}$,即x=0时,函数f(x)取得最小值,且最小值为$-\frac{1}{2}$;
当$2x-\frac{π}{6}=\frac{π}{2}$,即$x=\frac{π}{3}$时,函数f(x)取得最大值,且最大值为1.
所以函数f(x)在$[{0,\frac{2π}{3}})$上的最大值为1,最小值为$-\frac{1}{2}$;
(2)由(1)知$f(A)=sin({2A-\frac{π}{6}})=1$.
因为$A∈({0,\frac{π}{2}})$,$2A-\frac{π}{6}∈({-\frac{π}{6},\frac{5π}{6}})$,
所以$2A-\frac{π}{6}=\frac{π}{2}$,$A=\frac{π}{3}$.
由a2=b2+c2-2bccosA,得$12={b^2}+16-2×4b×\frac{1}{2}$,
即b2-4b+4=0,解得b=2.
故$S=\frac{1}{2}bcsinA=\frac{1}{2}×2×4×sin\frac{π}{3}=2\sqrt{3}$.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,正弦定理,三角形面积公式的应用,属于基本知识的考查.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{2}$或$\sqrt{10}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
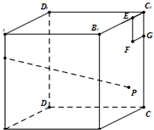 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 非体育迷 | 体育迷 | 总计 | |
| 男 | 30 | 15 | 45 |
| 女 | 45 | 10 | 55 |
| 总计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
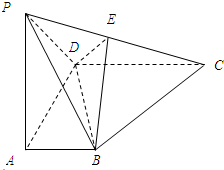 如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点
如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com