练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．若z=2+i，则$\frac{4i}{z\overline z-1}$=（　　）
    A．1B．-1C．iD．-i

    分析 直接利用复数的代数形式混合运算法则化简求解即可．

    解答 解：z=2+i，z•$\overline{z}$=（2+i）（2-i）=5，
    则$\frac{4i}{z\overline z-1}$=$\frac{4i}{5-1}=i$．
    故选：C．

    点评 本题考查复数的基本运算，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

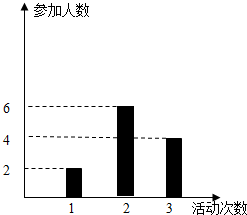    7．某城市号召中学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该城市某学校学生会共有12名学生，他们参加活动的次数统计如图所示．
    （Ⅰ）从学生会中任意选两名学生组成一个小组，若这两人参加活动次数恰好相等，则称该小组为“和谐小组”，求任选该校两名学生会成员组成的小组是“和谐小组”的概率；
    （Ⅱ）用样本估计总体，从该城市的中学生中任选4个小组（每小组两人），求这4个小组中“和谐小组”的组数X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在用数学归纳法证明不等式$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$≥$\frac{13}{24}$（n≥2）的过程中，当由n=k推到n=k+1时，不等式左边应（　　）
    A．增加了$\frac{1}{2（k+1）}$B．增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$
    C．增加了$\frac{1}{2k+1}$+$\frac{1}{2k+2}$，但减少了$\frac{1}{k+1}$D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

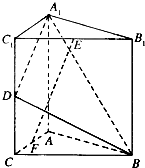    5．如图，在直三棱柱ABC-A1B1C1中，C1C=CB=CA=2，AC⊥CB，D，E分别为棱C1C，B1C1的中点．
    （1）求二面角B-A1D-A的平面角的余弦值；
    （2）在线段AC上是否存在一点F，使得EF⊥平面A1BD？若存在，确定点F的位置并证明结论；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=-xlnx+ax，g（x）=$\frac{1}{1+x}$．
    （1）若a=2，求函数f（x）的单调区间，并求f（x）的最大值；
    （2）若不等式f（x）≤g（x）对任意实数x∈[1，+∞）恒成立，求实数a的取值范围；
    （3）求证：不等式$\sum_{k=1}^{n}$lnk≥n（$\frac{1}{2}$-$\frac{1}{n+1}$）（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知两条平行直线l1：$\sqrt{3}$x-y+1=0与l2：$\sqrt{3}$x-y+3=0．
    （1）若直线n与l1、l2都垂直，且与坐标轴构成的三角形的面积是2$\sqrt{3}$，求直线n的方程．
    （2）若直线m经过点（$\sqrt{3}$，4），且被l1、l2所截得的线段长为2，求直线m的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．命题“?x∈R，|x|+x2≥0”的否定是（　　）
    A．?x0∈R，|x0|+x${\;}_{0}^{2}$≥0B．?x0∈R，|x0|+x${\;}_{0}^{2}$＜0
    C．?x∈R，|x|+x2＜0D．?x∈R，|x|+x2≤0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，已知椭圆 C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）左顶点为A1，右焦点为F2，过点 F2作垂直于x轴的直线交椭圆C于M、N两点，直线 A1M的斜率为$\frac{1}{2}$
    （Ⅰ）求椭圆C的离心率；
    （Ⅱ）若椭圆C的长轴长为4，点P（1，1），则在椭圆C上是否存在不重合两点D，E，使$\overrightarrow{OP}$=$\frac{1}{2}$（$\overrightarrow{OD}$+$\overrightarrow{OE}$）（O是坐标原点），若存在，求出直线DE的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．以下说法错误的是（　　）
    A．命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0”
    B．“x=-1”是“x2-5x-6=0”的根的逆命题为假命题
    C．若p∧q为假命题，则p、q均为假命题
    D．若命题p：?x∈R，使得x2+x+1＜0，则￢p：?x∈R，则x2+x+1≥0

    查看答案和解析>>

    同步练习册答案