3．为了对某班学生的数学、物理成绩进行分析，从该班25位男同学，15位女同学中随机抽取一个容量为8的样本．
（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出算式，不必计算出结果）；
（2）若这8人的数学成绩从小到大排序是65，68，72，79，81，88，92，95．物理成绩从小到大排序是72，77，80，84，86，90，93，98．
①求这8人中恰有3人数学、物理成绩均在85分以上的概率（结果用分数表示）；
②已知随机抽取的8人的数学成绩和物理成绩如表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
若以数学成绩为解释变量x，物理成绩为预报变量y，求y关于x的线性回归方程（系数精确到0.01）；并求数学成绩对于物理成绩的贡献率R
2（精确到0.01）．
参考公式：相关系数：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，R
2=r
2，
回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据：$\overline{x}$=80，$\overline{y}$=85，$\sum_{i=1}^{8}$（x
i-$\overline{x}$）
2=868，$\sum_{i=1}^{8}$（y
i-$\overline{y}$）
2═518，$\sum_{i=1}^{8}$（x
i-$\overline{x}$）（y
i-$\overline{y}$）=664，$\sqrt{868}$≈29.5，$\sqrt{518}$≈22.8．
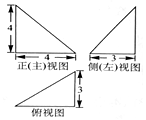某四面体三视图如图所示，该四面体的体积为（ ）
阅读快车系列答案
