
分析 由题意画出图形,求出正四棱锥的斜高,进一步求出高,代入棱锥体积公式得答案.
解答 解:如图,∵P-ABCD为正四棱锥,且底面边长为2,
过P作PG⊥BC于G,作PO⊥底面ABCD,垂足为O,连接OG.
由侧面积为12,即4×$\frac{1}{2}×2×PG=12$,即PG=3.
在Rt△POG中,PO=$\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2}$
∴正四棱锥的体积为V=$\frac{1}{3}×{s}_{ABCD}×PO=\frac{8\sqrt{2}}{3}$
故答案为:$\frac{8\sqrt{2}}{3}$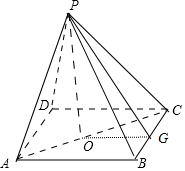
点评 本题考查棱锥体积的求法,考查数形结合的解题思想方法,是中档题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥4或m≤-2 | B. | m≥2或m≤-4 | C. | -2<m<4 | D. | -4<m<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某地区数学考试的成绩X服从正态分布X~N(μ,σ2),正态分布密度函数为$f(x)=\frac{1}{{\sqrt{2π}σ}}{e^{-\frac{{{{(x-σ)}^2}}}{{2{x^2}}}}}$,x∈(-∞,+∞),其密度曲线如图所示,则成绩X位于区间(86,94]的概率是0.0215.(结果保留3为有效数字)本题用到参考数据如下:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.
某地区数学考试的成绩X服从正态分布X~N(μ,σ2),正态分布密度函数为$f(x)=\frac{1}{{\sqrt{2π}σ}}{e^{-\frac{{{{(x-σ)}^2}}}{{2{x^2}}}}}$,x∈(-∞,+∞),其密度曲线如图所示,则成绩X位于区间(86,94]的概率是0.0215.(结果保留3为有效数字)本题用到参考数据如下:P(μ-σ<X≤μ+σ)=0.6826,P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-3σ<X≤μ+3σ)=0.9974.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com