
已知某公司生产某品牌服装的年固定成本为10万元,每生产千件需另投入2.7万元,设该公司年内共生产该品牌服装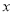 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为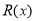 万元,且
万元,且 .
.
(Ⅰ)写出年利润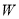 (万元)关于年产品
(万元)关于年产品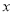 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
(注:年利润=年销售收入-年总成本)
(1) (2)当年产量为9千件时,该公司在这一品牌服装生产中获利最大.
(2)当年产量为9千件时,该公司在这一品牌服装生产中获利最大.
【解析】
试题分析:(1)利用基本不等式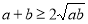 解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
解决实际问题时,应先仔细阅读题目信息,理解题意,明确其中的数量关系,并引入变量,依题意列出相应的函数关系式,然后利用基本不等式求解;(2)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(3)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.
试题解析:【解析】
(Ⅰ)当 时,
时,
当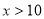 时,
时,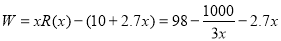
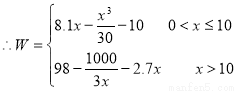 6分
6分
(Ⅱ)①当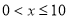 时,由
时,由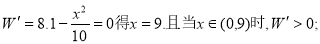
当
∴当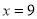 时,
时,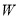 取最大值,且
取最大值,且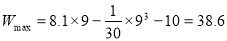 9分
9分
②当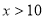 时,
时,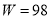
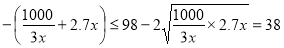
当且仅当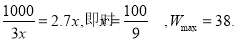 12分
12分
综合①、②知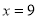 时,
时,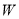 取最大值.
取最大值.
 所以当年产量为9千件时,该公司在这一品牌服装生产中获利最大. 13分
所以当年产量为9千件时,该公司在这一品牌服装生产中获利最大. 13分
考点:(1)求函数解析式;(2)基本不等式在实际的应用.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:2015届福建省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
已知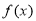 是定义在区间
是定义在区间 上的奇函数,且
上的奇函数,且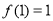 ,若
,若 时,有
时,有 .
.
(1)解不等式: ;
;
(2)若不等式 对
对 与
与 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数 ,则下列结论正确的是( ).
,则下列结论正确的是( ).
A.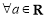 ,
,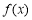 有唯一零点
有唯一零点
B.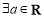 ,
,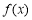 的最小值为
的最小值为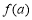
C.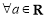 ,
,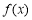 有极大值和极小值
有极大值和极小值
D.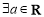 ,
,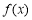 在
在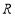 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:填空题
以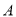 表示值域为
表示值域为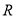 的函数组成的集合,
的函数组成的集合,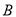 表示具有如下性质的函数
表示具有如下性质的函数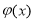 组成的集合:对于函数
组成的集合:对于函数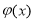 ,存在一个正数
,存在一个正数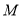 ,使得函数
,使得函数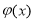 的值域包含于区间
的值域包含于区间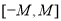 .例如,当
.例如,当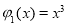 ,
,
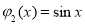 时,
时,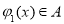 ,
,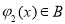 .现有如下命题:
.现有如下命题:
①设函数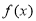 的定义域为
的定义域为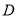 ,则“
,则“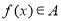 ”的充要条件是“
”的充要条件是“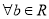 ,
,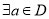 ,
,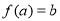 ”;
”;
②函数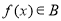 的充要条件是
的充要条件是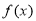 有最大值和最小值;
有最大值和最小值;
③若函数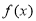 ,
,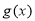 的定义域相同,且
的定义域相同,且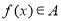 ,
,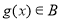 ,则
,则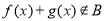 ;
;
④若函数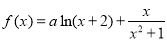 (
(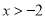 ,
,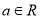 )有最大值,则
)有最大值,则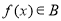 .
.
其中的真命题有 (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考理科数学试卷(解析版) 题型:选择题
箱子里有 个黑球,
个黑球,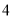 个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第
个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第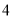 次取球之后停止的概率为
次取球之后停止的概率为
A. B.
B.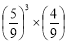 C.
C.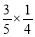 D.
D.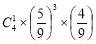
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:填空题
设等差数列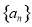 的前n项和为
的前n项和为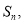 则
则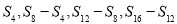 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列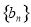 的前n项积为
的前n项积为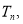 则
则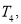 , ,
, ,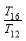 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
已知中心在原点的双曲线的渐近线方程是 ,且双曲线过点
,且双曲线过点
(Ⅰ)求双曲线的方程;
(Ⅱ)过双曲线右焦点 作倾斜角为
作倾斜角为 的直线交双曲线于
的直线交双曲线于 ,求
,求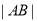 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com