
| A、255 | B、85 |
| C、255或-85 | D、255或85 |
| 32 |
| 8 |
| a4 |
| q3 |
| a1(1-q8) |
| 1-q |
| 1(1-28) |
| 1-2 |
| a1(1-q8) |
| 1-q |
| -1(1-(-2)8) |
| 1+2 |
| 16 |
| -8 |


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
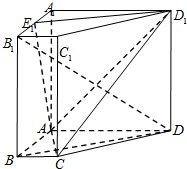 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
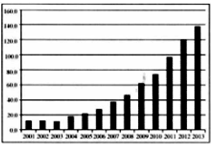 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A、y=ax2+bx+c |
| B、y=aex+b |
| C、y=eax+b |
| D、y=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 3n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com