
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,不等式
,不等式![]() 有且只有两个整数解,求
有且只有两个整数解,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减。
单调递减。
(2)![]()
【解析】
(1)对函数求导,根据a的不同范围,分别求出导函数何时大于零,何时小于零,这样就可以判断出函数的单调性。
(2)不等式![]() 可以化成
可以化成![]() ,构造函数
,构造函数![]() ,
,
求导数和单调性,结合条件分别讨论![]() ,三种情况下,可以求出满足条件的a的取值范围。
,三种情况下,可以求出满足条件的a的取值范围。
(1)函数的定义域为![]()
![]()
② 当![]() 时,
时,![]() 函数
函数![]() 在
在![]() 上是减函数;
上是减函数;
②当![]() 时,
时,![]() ,当
,当![]() 时
时![]() ,函数单调递增,
,函数单调递增,
当![]() 时,
时,![]() ,函数单调递减。
,函数单调递减。
③当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,函数递减,
,函数递减,
当![]() 时,
时,![]() ,函数单调递增。
,函数单调递增。
综上所述:当![]() 时,函数
时,函数![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减。
单调递减。
(2)![]()
![]()
![]()
令![]() ,求导得
,求导得![]() 令
令![]()
![]() 所以
所以![]() 是R上的增函数,而
是R上的增函数,而![]()
说明函数![]() 在R上存在唯一零点
在R上存在唯一零点![]()
此时函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]()

易证![]() ,
,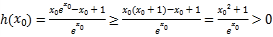
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
(1)若![]() 时,
时,![]() ,此时
,此时![]() 有无穷多个整数解,不符合题意;
有无穷多个整数解,不符合题意;
(2)若![]() 时,即
时,即![]() ,因为函数
,因为函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
所以![]() 时,
时,![]() ,所以
,所以![]() 无整数解,不符合题意;
无整数解,不符合题意;
(3)当![]() ,即
,即![]() 此时
此时![]() , 故0,1是
, 故0,1是![]() 的两个整数解,
的两个整数解,
又![]() 只有两个正整数解,因此
只有两个正整数解,因此 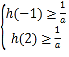 ,解得
,解得![]() 所以
所以![]()
综上所述![]() 的取值范围为
的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即![]() .设函数
.设函数![]() ,二次函数
,二次函数![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,则
的图象有且只有一个公共点,则![]() 的取值不可能是( )
的取值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题不正确的是( )
A.研究两个变量相关关系时,相关系数r为负数,说明两个变量线性负相关
B.研究两个变量相关关系时,相关指数R2越大,说明回归方程拟合效果越好.
C.命题“x∈R,cosx≤1”的否定命题为“x0∈R,cosx0>1”
D.实数a,b,a>b成立的一个充分不必要条件是a3>b3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P—ABCD的底面ABCD是平行四边形,PA⊥面ABCD,M是AD的中点,N是PC的中点.

(1)求证:MN∥面PAB;
(2)若平面PMC⊥面PAD,求证:CM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有高三文科学生1000人,统计其高三上期期中考试的数学成绩,得到频率分布直方图如下:
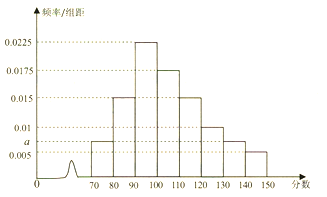
(1)求出图中![]() 的值,并估计本次考试低于120分的人数;
的值,并估计本次考试低于120分的人数;
(2)假设同组的每个数据可用该组区间的中点值代替,试估计本次考试不低于120分的同学的平均数(其结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com