
����Ŀ���������ʹ�˱���˼����������˵õ��ǻ�����������������Ȼ�����鼮���Ļ�����Ҫ���壬�����dzм��Ļ�����Ҫ��ʽij����Ϊ�˽�ѧ������ʱ��Ķ�������������ȡ��![]() ��ѧ�����е��飬���ݵ���õ���ѧ���վ��������ʱ����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����վ��������ʱ�䲻����
��ѧ�����е��飬���ݵ���õ���ѧ���վ��������ʱ����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����վ��������ʱ�䲻����![]() ���ӵ�ѧ����Ϊ������֮�������վ��������ʱ�����
���ӵ�ѧ����Ϊ������֮�������վ��������ʱ�����![]() ���ӵ�ѧ����Ϊ���Ƕ���֮����:��֪��ȡ���������վ��������ʱ�����
���ӵ�ѧ����Ϊ���Ƕ���֮����:��֪��ȡ���������վ��������ʱ�����![]() ���ӵ���
���ӵ���![]() ��
��
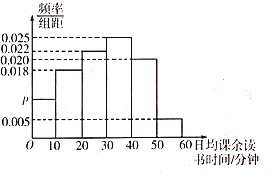
(1)��![]() ��ֵ;
��ֵ;
(2)������֪������������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() ���ϵİ�����Ϊ������֮�������Ա��й�?
���ϵİ�����Ϊ������֮�������Ա��й�?
�Ƕ���֮�� | ����֮�� | �ܼ� | |
�� | |||
Ů |
|
| |
�ܼ� |
(3)�������������õ���Ƶ����Ϊ���ʣ��ִӸõ�������ѧ���У������ȡ![]() ��ѧ����ÿ�γ�ȡ
��ѧ����ÿ�γ�ȡ![]() ������֪ÿ�����Ƿ鵽����Ӱ�죬�DZ���ȡ��������֮��������Ϊ�������
������֪ÿ�����Ƿ鵽����Ӱ�죬�DZ���ȡ��������֮��������Ϊ�������![]() ����
����![]() �ķֲ��к�����
�ķֲ��к�����![]()
����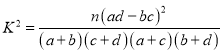 ������
������![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���𰸡���1��![]() ,n=100,��2������������û��
,n=100,��2������������û��![]() ���ϵİ�����Ϊ������֮�������Ա��йأ�3���ֲ��м�������
���ϵİ�����Ϊ������֮�������Ա��йأ�3���ֲ��м�������![]()
��������
��1�����ȸ���Ƶ�ʺ�Ϊ1��![]() ���ٸ���Ƶ�ʣ�Ƶ�������������Ĺ�ϵ��
���ٸ���Ƶ�ʣ�Ƶ�������������Ĺ�ϵ��![]() ��
��
��2�����ȼ��㡰����֮�ǡ���������Ȼ����������д![]() �������������ݹ�ʽ����
�������������ݹ�ʽ����![]() ��
��![]() �Ƚϴ�С�������жϣ�
�Ƚϴ�С�������жϣ�
��3���Ӹõ���ѧ���г�ȡһ��ѧ����������֮�����ĸ���Ϊ![]() ���������֪
���������֪![]()
����ֲ��к���ѧ����.
��1��![]()
��ã�![]() ��
��
����![]() .
.
(2)��Ϊ![]() ������������֮������
������������֮������![]()
�Ӷ�![]() ����������ͼ��ʾ:
����������ͼ��ʾ:
�Ƕ���֮�� | ����֮�� | �ܼ� | |
�� |
|
|
|
Ů |
|
|
|
�ܼ� |
|
|
|
��![]() �������е����ݴ��빫ʽ�����
�������е����ݴ��빫ʽ�����
![]()
��Ϊ![]() ������û��
������û��![]() ���ϵİ�����Ϊ������֮�������Ա��й�
���ϵİ�����Ϊ������֮�������Ա��й�
(3)��Ƶ����Ϊ���ʣ����Ӹõ���ѧ���г�ȡһ��ѧ����������֮�����ĸ���Ϊ![]() .
.
�������֪![]()
����![]()
![]() ��
��
![]()
![]()
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
|
|
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() ��������������
��������������![]() ��ʹ�ö������
��ʹ�ö������![]() ������
������![]() ���������dzƺ���
���������dzƺ���![]() Ϊ��
Ϊ��![]() ͬ�Ȳ�����������
ͬ�Ȳ�����������
��1����֤��������������![]() ��
��![]() ��������
��������![]() ͬ�Ȳ�����������
ͬ�Ȳ�����������
��2��������![]() ����
����![]() ͬ�Ȳ�������������
ͬ�Ȳ�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���Ƿ����������![]() ��ʹ�ú���
��ʹ�ú���![]() Ϊ��
Ϊ��![]() ͬ�Ȳ����������������ڣ���
ͬ�Ȳ����������������ڣ���![]() ��ȡֵ��Χ���������ڣ���˵�����ɣ�
��ȡֵ��Χ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����2acosB��2c��b��
��1�����A�Ĵ�С��
��2������ABC�����Բ�İ뾶Ϊ![]() �����Ϊ
�����Ϊ![]() �����ABC���ܳ���
�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˹���ְԱ�������飬ij��˾��ÿλְԱһ�����Ĺ���ҵ�����½��п�����֣����հ���ְԱ����ƽ��ֵ��ѡ��˾���ְԱ��������Ӧ����.��ְ֪Ա![]() һ�����Ĺ���ҵ�������ľ�Ҷͼ��ͼ��ʾ��
һ�����Ĺ���ҵ�������ľ�Ҷͼ��ͼ��ʾ��
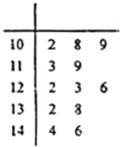
��1������ְԱ![]() ��ҵ����Ҷͼ�������һ��Ĺ���ҵ������λ����ƽ������
��ҵ����Ҷͼ�������һ��Ĺ���ҵ������λ����ƽ������
��2������ְԱ![]() ��ҵ���ߣ�����˾��Ϊ������ְԱ���ڹ�˾�����ͨ���齱��ʽ��ȡ����.��˾�������ſ�Ƭ������һ�ſ�Ƭ�ϱ�ע����Ϊ6ǧԪ�����ſ�Ƭ�Ľ���Ϊ4ǧԪ���������ŵĽ���Ϊ2ǧԪ.�����ǣ���ְԱ
��ҵ���ߣ�����˾��Ϊ������ְԱ���ڹ�˾�����ͨ���齱��ʽ��ȡ����.��˾�������ſ�Ƭ������һ�ſ�Ƭ�ϱ�ע����Ϊ6ǧԪ�����ſ�Ƭ�Ľ���Ϊ4ǧԪ���������ŵĽ���Ϊ2ǧԪ.�����ǣ���ְԱ![]() ��Ҫ�����ſ�Ƭ�����������ţ������ſ�Ƭ�ϵĽ����֮����Ϊ������.��ְԱ
��Ҫ�����ſ�Ƭ�����������ţ������ſ�Ƭ�ϵĽ����֮����Ϊ������.��ְԱ![]() ��ý���6ǧԪ�ĸ��ʣ���˵����ý���6ǧԪ��8ǧԪ�ĸ������Խϴ�
��ý���6ǧԪ�ĸ��ʣ���˵����ý���6ǧԪ��8ǧԪ�ĸ������Խϴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2��2xsin��+1�Ķ�������Բx2+my2=1�ϣ�����������������ֻ����������m��ȡֵ��Χ��_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{bn}��ǰn���ΪTn����T4=4��b5=6.
��1��������{bn}��ͨ�ʽ��
��2����������n1��n2������nt��������5��n1��n2������nt������b3��b5��![]() ��
��![]() ������
������![]() �����ɵȱ����У�������{nt}��ͨ�ʽ��t������������
�����ɵȱ����У�������{nt}��ͨ�ʽ��t������������
��3���������⣺�ڹ��Ȳ�����1�ĵȱ�����{an}�У�ǰn���ΪSn����am��am+2��am+1�ɵȲ����У���Sm��Sm+2��Sm+1Ҳ�ɵȲ�����.���жϴ��������٣���֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ž����г��ķ�չ��Խ��Խ����ѡ��Ͷ�����ƽ�����Ϊ���Ƶ��ֶΣ����潫A�аѻƽ���Ϊ���Ʋ�Ʒ��Ͷ���˵��������ͳ������ͼ��ʾ.
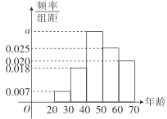
��1����ѻƽ���Ϊ���Ʋ�Ʒ��Ͷ���ߵ��������λ�����������С����ʾ��С���������λ��Ч���֣�
��2���ְ��շֲ�����ķ�����������![]() ��
��![]() ��Ͷ�����������ȡ5�ˣ��ٴ���5���������ȡ3�˽���Ͷ�ʵ��飬��ǡ��1��������
��Ͷ�����������ȡ5�ˣ��ٴ���5���������ȡ3�˽���Ͷ�ʵ��飬��ǡ��1��������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ǽ����һ�ڻ�����ߵ�![]() �����4�ף���͵�
�����4�ף���͵�![]() �����2�ף��۲��ߴӾ���ǽ
�����2�ף��۲��ߴӾ���ǽ![]() �ף�������
�ף�������![]() ��
��![]() �����ñڻ���������ӽ�
�����ñڻ���������ӽ�![]()
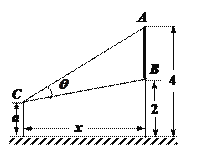
��1����![]() �ʣ��۲�����ǽ��Զʱ���ӽ�
�ʣ��۲�����ǽ��Զʱ���ӽ�![]() ���
���
��2����![]() ��
��![]() �仯ʱ����
�仯ʱ����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com