
【题目】已知 ![]() ,
, ![]() :
: ![]() ,
, ![]() :
: ![]() .
.
(1)若 ![]() 是
是 ![]() 的充分条件,求实数
的充分条件,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() ,“
,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数
”为假命题,求实数 ![]() 的取值范围.
的取值范围.
【答案】(1) 实数 ![]() 的取值范围是
的取值范围是 ![]() ;(2) 实数
;(2) 实数 ![]() 的取值范围为
的取值范围为 ![]() .
.
【解析】试题分析:(1)解命题![]() 的不等式可得命题
的不等式可得命题![]() 的充要条件
的充要条件![]() ,因为
,因为![]() 是
是 ![]() 的充分条件,所以两命题
的充分条件,所以两命题![]() 的范围构成的集合关系是
的范围构成的集合关系是![]() 是
是 ![]() 的子集,可得区间端点的关系
的子集,可得区间端点的关系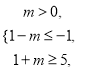 ,解不等式组可求得实数
,解不等式组可求得实数 ![]() 的取值范围是
的取值范围是 ![]() .(2)由已知“
.(2)由已知“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,可得命题
”为假命题,可得命题![]() 和命题
和命题 ![]() 一真一假,有
一真一假,有![]() 真
真 ![]() 假与
假与![]() 假
假 ![]() 真两种情况,分别得不等式组
真两种情况,分别得不等式组![]() 与
与![]() ,分别求解,可求得实数
,分别求解,可求得实数 ![]() 的取值范围为
的取值范围为 ![]() .
.
试题解析:(1) 由题知 ![]() :
: ![]() .
.
因为 ![]() 是
是 ![]() 的充分条件,所以
的充分条件,所以 ![]() 是
是 ![]() 的子集,
的子集,
所以 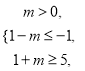 解得
解得 ![]() .所以实数
.所以实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
(2) 当 ![]() 时,
时, ![]() :
: ![]() ,依题意得,
,依题意得, ![]() 与
与 ![]() 一真一假.
一真一假.
当 ![]() 真
真 ![]() 假时,有
假时,有 ![]() 无解;
无解;
当 ![]() 假
假 ![]() 真时,有
真时,有 ![]() 解得
解得 ![]() 或
或 ![]() .
.
所以实数 ![]() 的取值范围为
的取值范围为 ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知△DEF三边所在的直线分别为l1:x=-2,l2:x+![]() y-4=0,l3:x-
y-4=0,l3:x-![]() y-4=0,⊙C为△DEF的内切圆.
y-4=0,⊙C为△DEF的内切圆.
(1)求⊙C的方程;
(2)设⊙C与x轴交于A、B两点,点P在⊙C内,且满足![]() .记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
.记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P点到两定点D(﹣2,0),E(2,0)连线斜率之积为- ![]() .
.
(1)求证:动点P恒在一个定椭圆C上运动;
(2)过 ![]() 的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
的直线交椭圆C于A,B两点,过O的直线交椭圆C于M,N两点,若直线AB与直线MN斜率之和为零,求证:直线AM与直线BN斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①函数![]() 的单调增区间是
的单调增区间是![]() ;
;
②若函数![]() 定义域为
定义域为![]() 且满足
且满足![]() ,则它的图象关于
,则它的图象关于![]() 轴对称;
轴对称;
③函数![]() 的值域为
的值域为![]() ;
;
④函数![]() 的图象和直线
的图象和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值可能是
的值可能是![]() ;
;
⑤若函数![]() 在
在![]() 上有零点,则实数
上有零点,则实数![]() 的取值范围是
的取值范围是![]() .
.
其中正确的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com