
分析 设侧棱长为l,两对角线分别为c,d,由条件建立方程组,消去c,d,用对角面的面积,求解表示侧面积.
解答  解:设侧棱长为h,两对角线分别为c,d.
解:设侧棱长为h,两对角线分别为c,d.
则$\left\{\begin{array}{l}ch=50\sqrt{2}\\ dh=10\sqrt{14}\\{(\frac{1}{2}c)}^{2}+{(\frac{1}{2}d)}^{2}=64\end{array}\right.$,可得c=$\frac{50\sqrt{2}}{h}$,
由(2)得d=$\frac{10\sqrt{14}}{h}$,代入${(\frac{1}{2}c)}^{2}+{(\frac{1}{2}d)}^{2}=64$得:${(\frac{25\sqrt{2}}{h})}^{2}+{(\frac{5\sqrt{14}}{h})}^{2}=64$,
∴64h2=625×2+25×14,∴S侧=4×8h=$\sqrt{1600}$=4×40=160.
直棱柱的侧面积:160.
点评 本题考查直四棱柱的定义、侧面积的求法,以及菱形的对角线的性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若AC与BD共面,则AD与BC也共面 | |
| B. | 若AC与BD是异面直线,则AD与BC也是异面直线 | |
| C. | 若AC与BD是相交直线,则AD与BC也是相交直线 | |
| D. | 若A,B,C,D不共面,则AC与BD既不平行也不相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
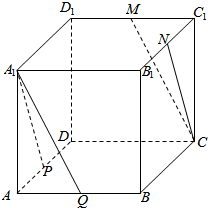 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
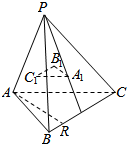 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com