Question

15．一轮渡向北以航速20km/h航行，此时风从西方吹来，风速5m/s，用作图法求轮渡的实际航行速度和方向．

Answer 1

分析 如图所示，设$\overrightarrow{{v}_{1}}$为轮渡原来航速，$\overrightarrow{{v}_{2}}$为风速，$\overrightarrow{v}$为轮渡的实际航行速度．则$|\overrightarrow{{v}_{1}}|$=20km/h，$|\overrightarrow{{v}_{2}}|$=5m/s=18km/h，则$|\overrightarrow{v}|$=$\sqrt{|\overrightarrow{{v}_{1}}{|}^{2}+|\overrightarrow{{v}_{2}}{|}^{2}}$.$tanθ=\frac{|\overrightarrow{{v}_{1}}|}{|\overrightarrow{{v}_{2}}|}$即可得出．

解答 解：如图所示，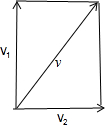
设$\overrightarrow{{v}_{1}}$为轮渡原来航速，$\overrightarrow{{v}_{2}}$为风速，$\overrightarrow{v}$为轮渡的实际航行速度．
则$|\overrightarrow{{v}_{1}}|$=20km/h，$|\overrightarrow{{v}_{2}}|$=5m/s=18km/h，
则$|\overrightarrow{v}|$=$\sqrt{|\overrightarrow{{v}_{1}}{|}^{2}+|\overrightarrow{{v}_{2}}{|}^{2}}$=$\sqrt{2{0}^{2}+1{8}^{2}}$=2$\sqrt{181}$km/h．
$tanθ=\frac{|\overrightarrow{{v}_{1}}|}{|\overrightarrow{{v}_{2}}|}$=$\frac{20}{18}$=$\frac{10}{9}$．
∴θ=arctan$\frac{10}{9}$．
∴轮渡的实际航行速度为2$\sqrt{181}$km/h，方向为北偏东$\frac{π}{2}$-arctan$\frac{10}{9}$．

点评 本题考查了向量夹角公式、数量积运算性质、向量共线定理，考查了推理能力与计算能力，属于中档题．