
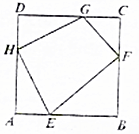
 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
分析 不妨设EF=a,FG=b,GH=c,HE=d,且设DG=x,GC=1-x,CF=y,FB=1-y,BE=z,AE=1-z,AH=t,DH=1-t.由勾股定理和二次函数的最值求法:配方,即可得到最小值.
解答 解:不妨设EF=a,FG=b,GH=c,HE=d,
且设DG=x,GC=1-x,CF=y,FB=1-y,
BE=z,AE=1-z,AH=t,DH=1-t.
则2a2+b2+2c2+d2=2[z2+(1-y)2]+[y2+(1-x)2]+2[x2+(1-t)2]+[t2+(1-z)2]
=[2z2+(1-z)2]+[y2+2(1-y)2]+[2x2+(1-x)2]+[t2+2(1-t)2]
=3(z-$\frac{1}{3}$)2+$\frac{2}{3}$+3(y-$\frac{2}{3}$)2+$\frac{2}{3}$+3(x-$\frac{1}{3}$)2+$\frac{2}{3}$+3(t-$\frac{2}{3}$)2+$\frac{2}{3}$,
当x=z=$\frac{1}{3}$,y=t=$\frac{2}{3}$时,取得最小值,且为$\frac{8}{3}$.
故选D.
点评 本题考查直角三角形的勾股定理和二次函数的最值的求法,考查运算能力,属于中档题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
设各项都是正数的等差数列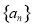 的公差为
的公差为 ,前
,前 项和为
项和为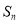 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com