练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设各项都是正数的等差数列的公差为，前项和为，若，，成等比数列，则（ ）

    A． B．

    C． D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=t+1}\\{y=2t}\end{array}\right.$（ 为参数），曲线C的参数方程为$\left\{\begin{array}{l}x=2{t}^{2}\\ y=2t\end{array}\right.$（t为参数）．试求直线l和曲线C的普通方程，并求出它们的公共点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：2017届辽宁庄河市高三9月月考数学（文）试卷（解析版） 题型：填空题

    直线被圆截得的弦长为，则___________．

    查看答案和解析>>

    科目：高中数学 来源：2017届辽宁庄河市高三9月月考数学（理）试卷（解析版） 题型：解答题

    为自然对数的底数.

    （Ⅰ）求函数在区间上的最值；

    （Ⅱ）当时，设函数（其中为常数）的3个极值点为，且，将这5个数按照从小到大的顺序排列，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源：2017届辽宁庄河市高三9月月考数学（理）试卷（解析版） 题型：填空题

    执行如图所示的程序框图，输出的值为___________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．集合P={x|$\frac{x-1}{x+3}$＞0}，Q={x|y=$\sqrt{4-{x}^{2}}$}，则P∩Q=（　　）
    A．（1，2]B．[1，2]C．（-∞，-3）∪（1，+∞）D．[1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知椭圆E的两焦点分别为（-1，0）（1，0），且经过点（1，$\frac{\sqrt{2}}{2}$）
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）过P（-2，0）的直线l交E于A、B两点，且$\overrightarrow{PB}$=3$\overrightarrow{PA}$，设A、B两点关于x轴的对称点分别是C、D，求四边形ACDB的外接圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

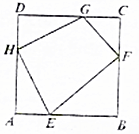    5．设四边形EFGH的四条边长为a，b，c，d，其四个顶点分别在单位正方形ABCD的四条边上，则2a2+b2+2c2+d2的最小值为（　　）
    A．3B．6C．$3\sqrt{2}$D．$\frac{8}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．如图，在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{6}}}{3}$，直线l与x轴交于点E，与椭圆C交于A、B两点．当直线l垂直于x轴且点E为椭圆C的右焦点时，弦AB的长为$\frac{{2\sqrt{6}}}{3}$．
    （1）求椭圆C的方程；
    （2）若点E的坐标为（$\frac{\sqrt{3}}{2}$，0），点A在第一象限且横坐标为$\sqrt{3}$，连结点A与原点O的直线交椭圆C于另一点P，求△PAB的面积；
    （3）是否存在点E，使得$\frac{1}{E{A}^{2}}$+$\frac{1}{E{B}^{2}}$为定值？若存在，请指出点E的坐标，并求出该定值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案