
分析 运用代入法,可将直线l和曲线C的参数方程化为普通方程,联立直线方程和抛物线方程,解方程可得它们的交点坐标.
解答 解:直线l的参数方程为$\left\{\begin{array}{l}{x=t+1}\\{y=2t}\end{array}\right.$( 为参数),
由x=t+1可得t=x-1,代入y=2t,
可得直线l的普通方程:2x-y-2=0.
曲线C的参数方程为$\left\{\begin{array}{l}{x=2{t}^{2}}\\{y=2t}\end{array}\right.$(t为参数),化为y2=2x,
联立$\left\{\begin{array}{l}{y=2(x-1)}\\{{y}^{2}=2x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-1}\end{array}\right.$,
于是交点为(2,2),$(\frac{1}{2},-1)$.
点评 本题主要考查了参数方程与普通方程的互化、直线与抛物线的位置关系等基础知识,考查了转化能力,属于基础题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:解答题
已知数列 .
.
(1)求这个数列的第10项;
(2) 是不是该数列中的项,为什么?
是不是该数列中的项,为什么?
(3)求证:数列中的各项都在区间(0,1)内;
(4)在区间 内有、无数列中的项?若有,有几项?若没有,说明理由.
内有、无数列中的项?若有,有几项?若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
设各项都是正数的等差数列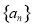 的公差为
的公差为 ,前
,前 项和为
项和为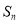 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com