
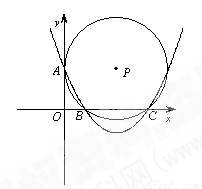
已知如图,抛物线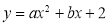 与x轴相交于B(
与x轴相交于B( ,0)、C(
,0)、C(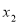 ,0) (
,0) (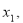
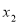
均大于0)两点, 与y轴的正半轴相交于A点. 过A、B、C三点的⊙P与y轴相切于点A,其面积为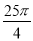 .
.
(1)请确定抛物线的解析式;
(2)M为y轴负半轴上的一个动点,直线MB交⊙P于点D.若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.(先画出符合题意的示意图再求解).
(1)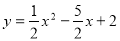 ;(2)
;(2)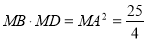 或
或 .
.
【解析】
试题分析: (1)首先由⊙P的面积为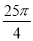 可知,圆半径
可知,圆半径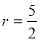 ,然后取出
,然后取出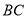 中点为E,连接
中点为E,连接 ,
, ,由圆心距的性质知
,由圆心距的性质知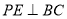 ,再由勾股定理和圆性质可求出
,再由勾股定理和圆性质可求出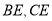 的长度,进而求出点
的长度,进而求出点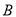 和点
和点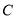 的坐标.最后将点
的坐标.最后将点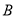 和点
和点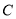 的坐标代入抛物线的方程得到方程组,求解之即可.
的坐标代入抛物线的方程得到方程组,求解之即可.
(2)根据弦切角定理可知,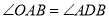 ,因此本小题可分两种情况:①当
,因此本小题可分两种情况:①当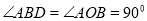 时,此时
时,此时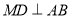 ,且AD是圆P的直径,可根据
,且AD是圆P的直径,可根据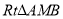 ∽
∽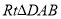 和
和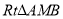 ∽
∽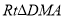 得出关于
得出关于 、
、 、
、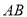 、
、 的对应成比例线段求出
的对应成比例线段求出 的长,然后根据切割线定理可得
的长,然后根据切割线定理可得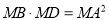 ,即可得出所求的值;②当
,即可得出所求的值;②当 时,思路与①相同,也是先求出
时,思路与①相同,也是先求出 的长,可根据直线
的长,可根据直线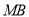 的解析式求出
的解析式求出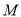 点的坐标,然后通过
点的坐标,然后通过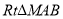 ∽
∽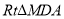 ,求出
,求出 的长,后面同①即可.
的长,后面同①即可.
试题解析:(1)根据题意知:圆半径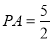 ,取
,取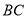 中点为E,连接
中点为E,连接 ,
, ,则
,则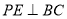 ,
,
且 ,
,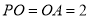 ,由勾股定理和圆性质知:
,由勾股定理和圆性质知: ,从而知:
,从而知: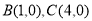 .
.
将B,C两点坐标代入抛物线方程可得:抛物线的解析式为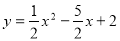 .
.
(2)根据题意知,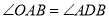 ,所以
,所以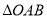 和
和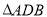 相似有两种情况:
相似有两种情况:
①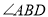 和
和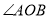 ,此时
,此时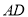 是
是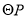 的直径,则
的直径,则 ,
, ,
,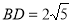
又因为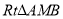 ∽
∽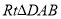 ,所以
,所以 ,即
,即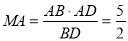 .
.
又因为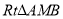 ∽
∽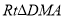 ,所以
,所以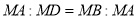 ,即
,即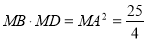 .
.
② 和
和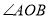 对应,此时BD是⊙P的直径,所以直线MB过P点.
对应,此时BD是⊙P的直径,所以直线MB过P点.
因为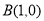 ,
, ,所以直线MB的解析式是:
,所以直线MB的解析式是: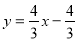 ,所以M点的坐标为
,所以M点的坐标为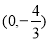 ,所以
,所以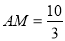 ,由
,由 ∽
∽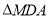 得,
得,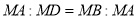 ,所以
,所以 .
.
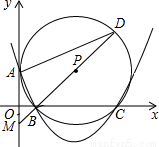

① ②
考点:抛物线的综合应用.


科目:高中数学 来源:2016届安徽省铜陵市高一5月月考数学试卷(解析版) 题型:选择题
等差数列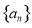 中,a1=1,d=3,an=298,则n的值等于( ).
中,a1=1,d=3,an=298,则n的值等于( ).
A.98 B. 100 C.99 D.101
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一自主招生考试数学试卷(解析版) 题型:选择题
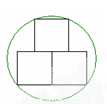
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
A.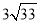 B.
B.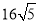 C.
C.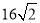 D.
D.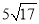
查看答案和解析>>
科目:高中数学 来源:2016届安徽省高一下学期期末考试数学试卷(解析版) 题型:选择题
为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为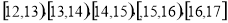 ,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图。已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
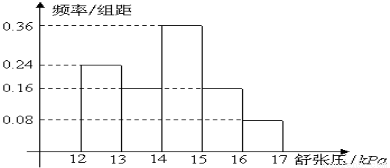
A.6 B.8 C.12 D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com