
分析 由题意作图辅助,通过椭圆的定义转化为求|PA|+|PF1|-4的最小值,从而解得.
解答 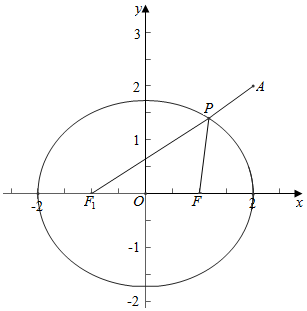 解:由题意作图象如右图,
解:由题意作图象如右图,
∵椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
∴a=2,c=1,b=$\sqrt{3}$;
∴|PF|+|PF1|=4,
∴|PA|-|PF|=|PA|-(4-|PF1|)
=|PA|+|PF1|-4,
故|PA|+|PF1|的最小值为$\sqrt{(2+1)^{2}+{2}^{2}}$=$\sqrt{13}$,
故|PA|-|PF|的最小值为$\sqrt{13}$-4,
故答案为:$\sqrt{13}$-4.
点评 本题考查了圆锥曲线的定义,同时考查了转化思想与数形结合的思想方法的应用.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1) | C. | (-1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$.平面ASD⊥平面SDC.
如图,四边形ABCD为平行四边形,且SD=2,SC=DC=AS=AD=$\sqrt{2}$.平面ASD⊥平面SDC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{2}$ | B. | $\frac{5\sqrt{2}}{3}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:填空题
书店举行购书优惠活动:①一次性购书不超过100元,不享受打折 优惠}②一次性购书超过100元但不超过200元,一律按原价打九 折;③一次性购书超过200元,一律按原价打七折.小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com