
分析 (1)先选两个元素作为一组再排列,恰有一个盒子中有2个小球,从4个小球中选两个作为一个元素,同另外两个元素在三个位置全排列,根据分步计数原理得到结果.
(2)先分类,把四个小球先分成两组,每组两个小球,或者是把四个小球分成两组,每组一个和三个,分完小组后再进行排列,从4个盒中选两个位置排列,得到结果.
解答 解:(1)根据题意,分三步进行分析:
第一步,从4个小球中取两个小球,有C42种方法;
第二步,将取出的两个小球放入一个盒内,有C41种方法;
第三步,在剩下的三个盒子中选两个放剩下的两个小球,有A32种方法;
由分步计数原理,共有C42•C41•A32=144种放法.
(2)根据题意,分2种情况讨论:
第一类,一个盒子放3个小球,一个盒子放1个小球,两个盒子不放小球有C41•C43•C31=48种方法;
第二类,有两个盒子各放2个小球,另两个盒子不放小球有C42•C42=36种方法;
由分类计数原理,共有48+36=84种放法.
点评 本题考查排列、组合的应用,涉及分类、分步计数原理的应用,关键是转化问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
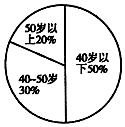 200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.
200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
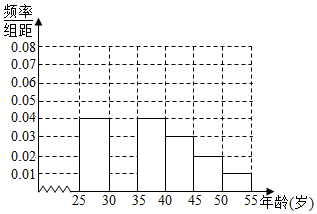
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com