
分析 (1)由导数求出函数的单调区间,由单调性求出函数的最大值;
(2)由f(x1)≤g(x2)恒成立,等价于f(x1)max≤g(x2)max,通过讨论a的范围,确定g(x)的单调区间,求出g(x)的最大值,从而求出a的范围.
解答 解:(1)∵f(x)=lnx-x+1,x∈(0,+∞),
∴f′(x)=$\frac{1-x}{x}$,
∴当0<x<1时,f′(x)>0,
当x>1时,f′(x)<0,
∴f(x)≤f(1)=0,
∴f(x)的最大值为0;
(2)若对?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,
依题意地f(x1)max≤g(x2)max,其中x1∈(0,+∞),x2∈[1,2],
由(1)知f(x1)max=f(1)=0
而g′(x)=3(x-a)(x+a),(a>0),
①0<a≤1时,x∈[1,2],g′(x)≥0恒成立,
∴g(x)在[1,2]递增,此时g(x)max=g(2)=8-6a2,
由题意得$\left\{\begin{array}{l}{8-{6a}^{2}≥0}\\{0<a≤1}\end{array}\right.$,
∴0<a≤1;
②1<a<2时,x∈(1,a),g′(x)<0,x∈(a,2),g′(x)>0,
∴g(x)在(1,a)递减,在(a,2)递增,
∴g(x)max=max{g(2),g(1)},
若g(1)>g(2),即1-3a2>8-6a2即a2>$\frac{7}{3}$,
此时1-3a2<0不合题意;
若g(1)≤g(2)即1-3a2≤8-6a2,即a2≤$\frac{7}{3}$,
∴1<a≤$\frac{\sqrt{21}}{3}$,
由题意得$\left\{\begin{array}{l}{8-{6a}^{2}≥0}\\{1<a≤\frac{\sqrt{21}}{3}}\end{array}\right.$,
∴1<a≤$\frac{2\sqrt{3}}{3}$,
③a≥2时,x∈[1,2],g′(x)≤0恒成立,
∴g(x)在[1,2]递减,
∴g(x)max=g(1)=1-3a2<0不合题意,
综上,a∈(0,$\frac{2\sqrt{3}}{3}$].
点评 本题考查了利用导数求函数的最值,运用等价转换思想求参数,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
 某工程队在南海海域进行填海造地工程,欲在边长为1千米的正三角形岛礁ABC的外围选择一点D(D在平面ABC内),建设一条军用飞机跑道AD,在点D测得B、C两点的视角∠BDC=60°,如图所示,记∠CBD=θ,如何设计θ,使得飞机跑道AD最长?
某工程队在南海海域进行填海造地工程,欲在边长为1千米的正三角形岛礁ABC的外围选择一点D(D在平面ABC内),建设一条军用飞机跑道AD,在点D测得B、C两点的视角∠BDC=60°,如图所示,记∠CBD=θ,如何设计θ,使得飞机跑道AD最长?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 0 | C. | 2 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
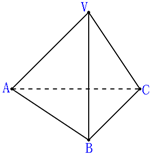 如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1则二面角V-AB-C的平面角的度数为( )
如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1则二面角V-AB-C的平面角的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
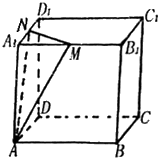 如图,在棱长为4的正方体ABCD-A1B1C1D1中,M、分别是棱A1B1、A1D1的中点,
如图,在棱长为4的正方体ABCD-A1B1C1D1中,M、分别是棱A1B1、A1D1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的体积为( )| A. | $8\sqrt{3}$ | B. | 8 | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com